Đề bài
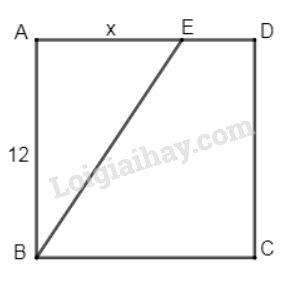
\(ABCD\) là một hình vuông cạnh \( 12cm\), \(AE = x(cm)\) (h.\(123\)). Tính \(x\) sao cho diện tích tam giác \(ABE\) bằng \(\dfrac{1}{3}\) diện tích hình vuông \(ABCD\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Công thức tính diện tích tam giác vuông: Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông.
+) Công thức tính diện tích hình vuông: Diện tích hình vuông bằng bình phương cạnh của nó.
Lời giải chi tiết
Diện tích tam giác vuông \(ABE\) là: \(S' = \dfrac{1}{2}AB.A{\rm{E}} = \dfrac{1}{2}.12.x = 6x\left( {c{m^2}} \right)\)
Diện tích hình vuông là: \(S = 12.12 = 144\left( {c{m^2}} \right)\)
Theo đề bài ta có: \(S' = \dfrac{S}{3}\)
\(\Rightarrow 6x = \dfrac{{144}}{3} \)
\(\Rightarrow 6x= 48\)
\( \Rightarrow x = 48:6 = 8\left( {cm} \right)\).
Vậy \(x = 8cm\).
dapandethi.vn
