Bài 13 trang 119 sgk toán lớp 8 tập 1

Đề bài

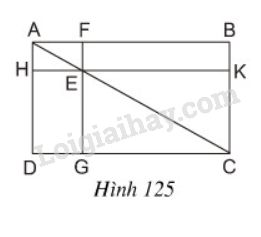
Cho hình \(125\), trong đó \(ABCD\) là hình chữ nhật, \(E\) là một điểm bất kì nằm trên đường chéo \(AC, FG // AD\), và \(HK // AB\).

Chứng minh rằng hai hình chữ nhật \(EFBK\) và \(EGDH\) có cùng diện tích. 

Lời giải chi tiết

\(ABCD\) là hình chữ nhật nên \(AB//CD;\;AD//BC\)

Vì \(FG// AD\) (gt) nên suy ra \(EG//KC\)

Vì \(HK//DC\) (vì cùng song song với \(AB\)) nên suy ra \(EK//GC\) 

\( \Rightarrow \) Tứ giác \(EKCG\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Mặt khác, \(\widehat {GCK} = {90^0}\) (gt) do đó \(EKCG\) là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

Xét \(\Delta ECG\) và \(\Delta CEK\) có:

+) \(EG=KC\) (vì \(EKCG\) là hình chữ nhật)

+) \(EC\) chung (gt)

+) \(EK=CG\) (vì \(EKCG\) là hình chữ nhật)

\(\Rightarrow \Delta ECG = \Delta CEK\) (c-c-c)

Do đó: \({S_{ECG}} = {S_{CEK}}\)    (1)   (Hai tam giác bằng nhau thì có diện tích bằng nhau)

Tương tự:

Vì \(ABCD\) là hình chữ nhật nên \(AB=DC, AD=BC, \widehat D=\widehat B=90^0\)

\(\Rightarrow \Delta ADC = \Delta CBA\) (c-g-c)

Do đó: \({S_{ ADC}} = {S_{CBA}}\)      (2)

Vì \(AF//HE, AH//EF\) nên \(AHEF\) là hình bình hành. Lại có \(\widehat A=90^0\) (do ABCD là hình chữ nhật) nên \(AHEF\) là hình chữ nhật. 

Suy ra \(AF=HE, AH=FE, \widehat H=\widehat F=90^0\) (tính chất)

\(\Rightarrow \Delta AHE = \Delta EFA\) (c-g-c)

Do đó: \({S_{AHE}} = {S_{ EFA}}\)       (3)

Ta có: 

\(\eqalign{
& {S_{ADC}} = {S_{AHE}} + {S_{EGDH}} + {S_{ECG}} \cr
& {S_{CBA}} = {S_{EFA}} + {S_{EFBK}} + {S_{CEK}} \cr} \)

Kết hợp với (2) \(\Rightarrow {S_{AHE}} + {S_{EGDH}} + {S_{ECG}} = {S_{EFA}} \)\(+ {S_{EFBK}} + {S_{CEK}}\) 

Kết hợp với (1) và (3) \(\Rightarrow {S_{EGDH}} = {S_{EFBK}}\)

dapandethi.vn