Đề bài
Cho đường tròn \((O ; R),\) điểm \(A\) nằm bên ngoài đường tròn \((R < OA < 3R).\) Vẽ đường tròn \((A ; 2R).\)
\(a)\) Hai đường tròn \((O)\) và \((A)\) có vị trí tương đối như thế nào đối với nhau\(?\)
\(b)\) Gọi \(B\) là một giao điểm của hai đường tròn trên. Vẽ đường kính \(BOC\) của đường tròn \((O).\) Gọi \(D\) là giao điểm ( khác \(C\)) của \(AC\) và đường tròn \((O)\). Chứng minh rằng \(AD = DC.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Nếu \(R – r < OO'< R + r\) thì đường tròn \((O)\) và đường tròn \((O')\) cắt nhau.
+) Trong tam giác cân, đường cao ứng với cạnh đáy cũng là đường phân giác, trung tuyến, trung trực.
Lời giải chi tiết
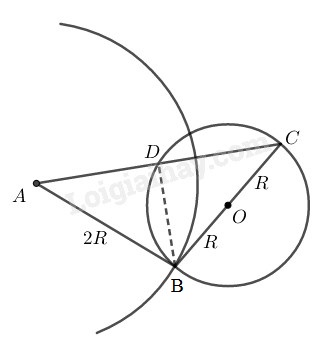
\(a)\) Ta có: \(R < OA < 3R \)\(⇔ 2R- R < OA < 2R + R\)
Suy ra hai đường tròn \((O; R)\) và \((A; 2R)\) cắt nhau.
\(b)\) Tam giác \(BCD\) nội tiếp trong đường tròn \((O)\) có \(BC\) là đường kính nên \(\widehat {BDC} = 90^\circ \)
Suy ra: \(BD ⊥ AC\)
Ta có: \(AB = 2R\) và \(BC = 2OB = 2R\)
Suy ra tam giác \(ABC\) cân tại \(B\;\; \)
Vì tam giác ABC cân tại B có BD là đường cao (do \(BD ⊥ AC\)) nên BD cũng là đường trung tuyến.
Suy ra: \(AD = DC.\)
dapandethi.vn
