Đề bài
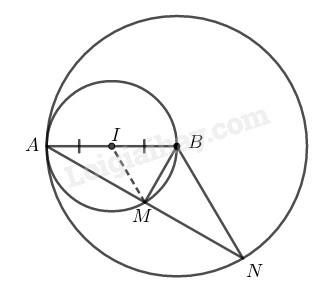
Cho \(I\) là trung điểm của đoạn thẳng \(AB.\) Vẽ các đường tròn \((I ; IA)\) và \((B ; BA)\)
\(a)\) Hai đường tròn \((I)\) và \((B)\) nói trên có vị trí tương đối như thế nào đối với nhau\(?\) Vì sao\(?\)
\(b)\) Kẻ một đường thẳng đi qua \(A,\) cắt các đường tròn \((I)\) và \((B)\) theo thứ tự tại \( M\) và \(N.\) So sánh các độ dài \(AM\) và \(MN.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Nếu \(OO' = R – r\) thì đường tròn \((O)\) và đường tròn \((O')\) tiếp xúc trong.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Lời giải chi tiết
\(a)\) Vì \(A, I , B\) thẳng hàng nên:
\(BI = AB – AI\)
Vậy đường tròn \((I ; IA)\) tiếp xúc với đường tròn \((B; BA)\) tại \(A.\)
\(b)\) Tam giác \(AMB\) nội tiếp trong đường tròn \((I)\) có \(AB\) là đường kính nên \(\widehat {AMB} = 90^\circ \)
Suy ra: \(AM ⊥ BM\) hay \(BM ⊥ AN\)
Xét đường tròn (B) có \(BM ⊥ AN\) mà BM là 1 phần đường kính và AN là dây cung
Suy ra: \(AM = MN\) ( đường kính vuông góc dây cung thì đi qua trung điểm của dây ấy).
dapandethi.vn
