Đề bài
Cho hai đường tròn đồng tâm \(O.\) Gọi \(AB\) là dây bất kỳ của đường tròn nhỏ. Đường thẳng \(AB\) cắt đường tròn lớn ở \(C\) và \(D\) \((A\) nằm giữa \(B\) và \(C).\) So sánh các độ dài \(AC\) và \(BD.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức: Trong một đường tròn:
+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Lời giải chi tiết
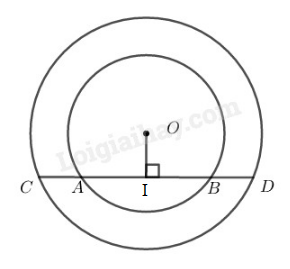
Kẻ \(OI ⊥ AB.\) Ta có: \(OI ⊥ CD\)
Trong đường tròn \((O)\) (nhỏ) ta có: \(OI ⊥ AB\)
Suy ra: \(IA = IB\) \((1)\) ( đường kính vuông góc dây cung thì đi qua trung điểm của dây ấy)
Trong đường tròn \((O)\) (lớn) ta có: \(OI ⊥ CD\)
Suy ra: \(IC = ID\) ( đường kính vuông góc dây cung thì đi qua trung điểm của dây ấy)
Hay \(IA + AC = IB + BD \) \( (2)\)
Từ \((1)\) và \((2)\) suy ra: \(AC = BD.\)
dapandethi.vn
