Đề bài
Cho tứ giác \(ABCD\) có \(AB = a , \widehat {CAB} = \alpha ,\)\( \widehat {DBA} = \beta , \widehat {DAC} = \alpha ' , \widehat {CBD} = \beta '\). Tính độ dài cạnh \(CD\).
Lời giải chi tiết
(h.62).
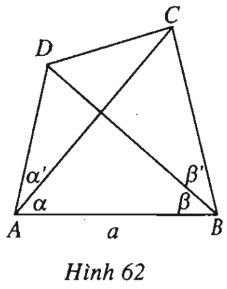
Tính \(AD\) và \(AC\) như bài 68 ta được
\(AD = \dfrac{{a\sin \beta }}{{\sin (\alpha + \alpha ' + \beta )}} , \)
\( AC = \dfrac{{a\sin (\beta + \beta ')}}{{\sin (\alpha + \beta + \beta ')}}\).
Sau đó áp dụng đính lí cosin vào tam giác \(ACD\) ta có
\(C{D^2} = A{C^2} + A{D^2} - 2AC.AD.\cos \alpha '\).
dapandethi.vn
