Đề bài
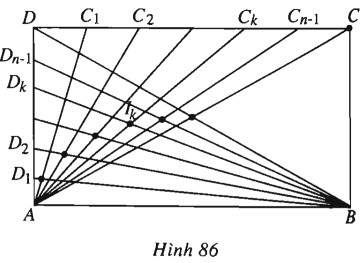
Trên hình 86, cạnh \(DC\) của hình chữ nhật \(ABCD\) được chia thành \(n\) đoạn thẳng bằng nhau bởi các điểm chia \(C_1, C_2,…,C_{n-1}\); cạnh \(AD\) cũng được chia thành \(n\) đoạn thẳng bằng nhau bởi các điểm chia \(D_1, D_2,…,D_{n-1}\). Gọi \(I_k\) là giao điểm của đoạn thẳng \(AC_k\) với đoạn thẳng \(BD_k\). Chứng minh rằng các điểm \(I_k\) (\(k=1,2,…,n-1\)) nằm trên elip có trục lớn là cạnh \(AB\), độ dài trục bé bằng chiều rộng \(AD\) của hình chữ nhật \(ABCD\).
Lời giải chi tiết
Chọn hệ trục tọa độ \(Oxy\) có: trục \(Ox\) đi qua \(A, B;\) trục \(Oy\) là đường trung trực của \(AB\). Đặt \(AB=2a, AD=2b\). Hãy tìm tọa độ của \(I_k\) và chứng minh \(I_k\) nằm trên elip có phương trình \( \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\).
dapandethi.vn
