Đề bài
Xác định tâm đối xứng, độ dài hai trục, tiêu cự, tâm sai, tọa độ các tiêu điểm và các đỉnh của mỗi elip sau:
a)\( \dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1 ;\)
b) \({x^2} + 4{y^2} = 1 ;\)
c) \(4{x^2} + 5{y^2} = 20 ;\)
d) \(4{x^2} + 16{y^2} - 1 = 0\)
e) \({x^2} + 3{y^2} = 2 ;\)
f) \(m{x^2} + n{y^2} = 1 (n > m > 0,m \ne n).\)
Vẽ elip có phương trình ở câu a).
Lời giải chi tiết
a) \(O\) là tâm đối xứng, \({a^2} = 25 \Rightarrow a = 5 ; \) \( {b^2} = 16 \Rightarrow b = 4 ;\) \( {c^2} = {a^2} - {b^2} = 9 \Rightarrow c = 3\).
Tâm sai \(e = \dfrac{c}{a} = \dfrac{3}{5}\).
Độ dài trục lớn : \(2a=10\), độ dài trục bé: \(2b=8\). Tiêu cự : \(2c=6\).
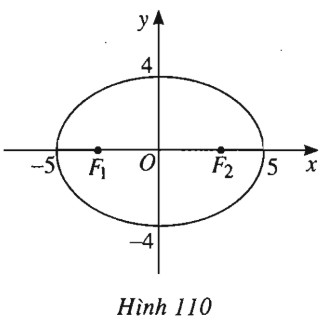
Các tiêu điểm : \({F_1}( - 3 ; 0) , {F_2}(3 ; 0)\). Các đỉnh: \(( \pm 5 ; 0) , (0 ; \pm 4)\).
Elip được vẽ như hình 110.
b) Viết lại phương trình của elip: \( \dfrac{{{x^2}}}{1} = \dfrac{{{y^2}}}{{ \dfrac{1}{4}}} = 1\). Elip có tâm đối xứng \(O\).
\({a^2} = 1 \Rightarrow a = 1 ;\) \( {b^2} = \dfrac{1}{4} \Rightarrow b = \dfrac{1}{2} ;\) \( {c^2} = {a^2} - {b^2} = \dfrac{3}{4} \Rightarrow c = \dfrac{{\sqrt 3 }}{2}\), tâm sai \(e = \dfrac{{\sqrt 3 }}{2}\).
Độ dài trục lớn : \(2a=2,\) độ dài trục bé : \(2b=1,\) tiêu cự : \(2c=\sqrt 3 \).
Các tiêu điểm: \({F_1}\left( { - \dfrac{{\sqrt 3 }}{2} ; 0} \right), {F_2}\left( { \dfrac{{\sqrt 3 }}{2} ; 0} \right)\). Các đỉnh : \(( \pm 1 ; 0) , \left( {0 ; \pm \dfrac{1}{2}} \right)\).
Các câu c), d), e), f) làm tương tự.
dapandethi.vn
