Đề bài
Cho tam giác cân \(ABC\) có \(\widehat B = {120^\circ},\) \(AC = 6cm.\) Tính độ dài đường tròn ngoại tiếp tam giác đó.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Trong giác cân, đường cao ứng với cạnh đáy cũng là đường trung tuyến ứng với cạnh đáy.
+) Trong một đường tròn, góc nội tiếp (nhỏ hơn hoặc bằng \(90^\circ\)) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
+) Độ dài \(C\) của một đường tròn bán kính \(R\) được tính theo công thức: \(C=2\pi R\)
Lời giải chi tiết
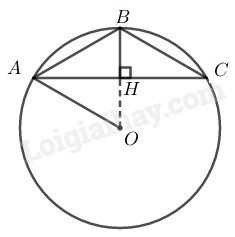
Vẽ đường tròn \((O)\) ngoại tiếp tam giác \(ABC\)
\(∆ABC\) cân có \(\widehat B = 120^\circ \) nên \(∆ABC\) cân tại \(B\)
\( \Rightarrow \widehat A = \widehat C = \displaystyle {{{{180}^\circ} - \displaystyle {{120}^\circ}} \over 2} = {30^0}\)
Kẻ \(BH \bot AC\)\( \Rightarrow AH = HC = \displaystyle {1 \over 2}AC = 3\) \((cm)\)
Trong tam giác vuông \(BHA\) ta có \(\widehat {BHA} = {90^0}\) có:
\(AB =\displaystyle {{AH} \over {\cos A}} \)\(=\displaystyle {3 \over {\cos {{30}^0}}} \)\(= \displaystyle {3 \over {\displaystyle {{\sqrt 3 } \over 2}}}\)\(= 2\sqrt 3 \;\;(cm)\)
Xét đường tròn \((O)\) có: \(\widehat C = \displaystyle {1 \over 2}\widehat {AOB}\) (hệ quả góc nội tiếp)
\( \Rightarrow \widehat {AOB} = 2\widehat C = {2.30^0} = {60^0}\)
\(OA = OB\) (bán kính)
Suy ra \(∆AOB\) đều nên \(OA = OB = 2\sqrt 3 \; (cm)\)
Độ dài đường tròn ngoại tiếp \(∆ABC\)
\(C = 2\pi R\)\( = 2\pi .2\sqrt 3 = 4\pi \sqrt 3 \) \((cm)\)
dapandethi.vn
