Cho hình lăng trụ đứng ABC.A’B’C’ mà đáy là tam giác vuông tại B có AB=a, BD=b, AA’=c\(\left( {{c^2} \ge {a^2} + {b^2}} \right).\) Một mặt phẳng \(\left( P \right)\) đi qua A và vuông góc với CA’.
LG a
Xác định thiết diện của hình lăng trụ khi cắt bởi \(mp\left( P \right).\)
Lời giải chi tiết:
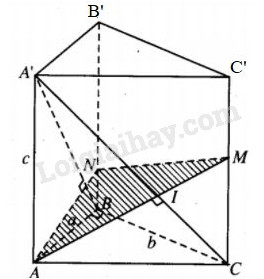
Trong \(mp\left( {AA'C'C} \right)\), dựng đường thẳng qua A vuông góc với CA’ lần lượt cắt CA’ và CC’ tại I và M.
Vì \(AC = \sqrt {{a^2} + {b^2}} \le c\) nên \(IC \le IA',\) do đó M phải thuộc đoạn CC’.
Bây giờ ta tìm giao điểm N và \(\left( P \right)\) và BB’. Dễ thấy \(AN \bot BC,AN \bot CA'\)
\( \Rightarrow AN \bot A'B.\) Vậy để tìm N, ta kẻ qua A (trong \(mp\left( {A'B'BA} \right)\)) đường thẳng vuông góc với A’B cắt B’B tại N.
Vậy thiết diện là tam giác AMN.
LG b
Tính diện tích thiết diện nói trên.
Lời giải chi tiết:
Ta có : \({V_{A'.AMN}} = {V_{M.AA'N}} \) \(= {V_{M.AA'B}} = {V_{C.A'AB}} = {1 \over 6}abc\)
(do \(NB//AA',MC// AA').\)
Mặt khác :
\({V_{A'.AMN}} = {1 \over 3}.{S_{AMN}}.A'I \)
\(\Rightarrow {S_{AMN}} = {{3{V_{A'.AMN}}} \over {A'I}} = {{abc} \over {2A'I}}.\)
Xét tam giác vuông A’AC ta có :
\(A'I.A'C = AA{'^2} = {c^2} \) \(\Rightarrow A'I = {{{c^2}} \over {A'C}} = {{{c^2}} \over {\sqrt {{a^2} + {b^2} + {c^2}} }}\).
Vậy \({S_{AMN}} = {{ab\sqrt {{a^2} + {b^2} + {c^2}} } \over {2c}}.\)
Loigiaihay.com
