Đề bài
Cho khối chóp tứ giác đều S.ABCD. Một mặt phẳng \(\left( \alpha \right)\) đi qua A, B và trung điểm M của cạnh SC. Tính tỉ số thể tích của hai phần khối chóp bị phân chia bởi mặt phẳng đó.
Lời giải chi tiết
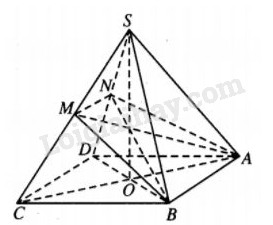
Kẻ \(MN//CD\left( {N \in SD} \right)\) thì hình thang \(ABMN\) là thiết diện của khối chóp khi cắt bởi \(mp\left( {ABM} \right)\). Ta có
\(\eqalign{ & {{{V_{S.ANB}}} \over {{V_{S.ADB}}}} = {{SN} \over {SD}} = {1 \over 2}\cr& \Rightarrow {V_{S.ANB}} = {1 \over 2}{V_{S.ADB}} = {1 \over 4}{V_{S.ABCD}}. \cr & {{{V_{S.BMN}}} \over {{V_{S.CBD}}}} = {{SM} \over {SC}}.{{SN} \over {SD}} = {1 \over 2}.{1 \over 2} = {1 \over 4} \cr & \Rightarrow {V_{S.BMN}} = {1 \over 4}{V_{S.CBD}} = {1 \over 8}{V_{S.ABCD}}. \cr} \)
Vậy \({V_{S.ABMN}} = {V_{S.ANB}} + {V_{S.BMN}} = {3 \over 8}{V_{S.ABCD}}\)
Do đó : \({{{V_{S.ABMN}}} \over {{V_{ABMNCD}}}} = {3 \over 5}.\)
dapandethi.vn
