Đề bài
Cho khối chóp tứ giác đều S.ABCD mà khoảng cách từ đỉnh A đến \(mp\left( {SBC} \right)\) bằng 2a. Với giá trị nào của góc giữa mặt bên và mặt đáy của khối chóp thì thể tích của khối chóp là nhỏ nhất ?
Lời giải chi tiết
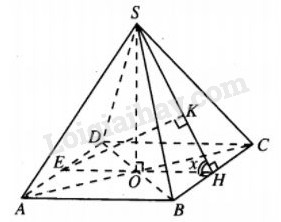
Giả sử O là tâm của hình vuông ABCD. Khi đó \(SO \bot \left( {ABCD} \right)\).
Gọi EH là đường trung bình của hình vuông ABCD \(\left( {E \in AD,H \in BC} \right).\)
Vì \(AD//BC\) nên \(AD//\left( {SBC} \right)\), do đó
\(d\left( {A,\left( {SBC} \right)} \right) = d\left( {E,\left( {SBC} \right)} \right)\)
Kẻ \(EK \bot SH\). Dễ thấy \(EK \bot \left( {SBC} \right)\) suy ra
\(EK = d\left( {A,\left( {SBC} \right)} \right) = 2a.\)
Ta có : \(BC \bot SH,BC \bot OH \Rightarrow \)\(\widehat {SHO}\) là góc giữa mặt bên \(\left( {SBC} \right)\) và mặt phẳng đáy. Đặt \(\widehat {SHO} =x\left( {0 < x < {\pi \over 2}} \right)\). Khi đó :
\(EH = {{2a} \over {{\mathop{\rm sinx}\nolimits} }};\;OH = {a \over {{\mathop{\rm s}\nolimits} {\rm{inx}}}};\;SO = {a \over {{\mathop{\rm s}\nolimits} {\rm{inx}}}}{\mathop{\rm tanx}\nolimits} = {a \over {{\mathop{\rm cosx}\nolimits} }}\)
Vậy: \({V_{S.ABCD}} = {1 \over 3}{S_{ABCD}}.SO = {{4{a^3}} \over {3\cos x{{\sin }^2}x}}\)
Từ đó \({V_{S.ABCD}}\) nhỏ nhất khi và chỉ khi \(y\left( x \right) = \cos x.{\sin ^2}x\) đạt giá trị lớn nhất. Ta có:
\(\eqalign{
y'\left( x \right) &= - {\sin ^3}x + 2\sin x.{\cos ^2}x \cr
& = \sin x\left( {2{{\cos }^2}x - {{\sin }^2}x} \right) \cr
& = \sin x\left( {2 - 3{{\sin }^2}x} \right) \cr
& = 3\sin x\left( {\sqrt {{2 \over 3}} - \sin x} \right)\left( {\sqrt {{2 \over 3}} + \sin x} \right) \cr} \)
Vì \(0 < x < {\pi \over 2}\) nên \(\sin x\left( {\sqrt {{2 \over 3}} + \sin x} \right) > 0\)
Gọi \(\alpha \) là góc sao cho \(\sin \alpha = \sqrt {{2 \over 3}} ;\,\,0 < \alpha < {\pi \over 2}\)
Ta có bảng biến thiên của hàm số \(y\left( x \right) = \cos x.{\sin ^2}x\):
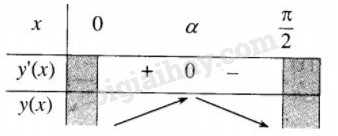
Vậy \({V_{S.ABCD}}\) đạt giá trị lớn nhất khi \(x = \alpha \) với \(0 < \alpha < {\pi \over 2}\) và \(\sin x = \sqrt {{2 \over 3}} .\)
Loigiaihay.com
