Đề bài
Cho tam giác ABC với BC=a, AC=b và AB=c.Kẻ đường phân giác AD, biết b’=DC, c’=DB. Đặt l=AD.
a) Tính l theo b, c, b’, c’.
b) Tính l theo a, b, c.
Lời giải chi tiết
(h.138).
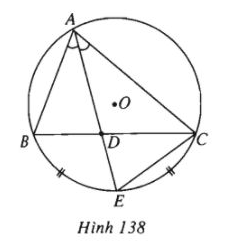
a) Gọi (O) là đường tròn ngoại tiếp tam giác ABC. Tia AD cắt (O) tại E. Ta có AD.DE=DB.DC, tức là \(l.DE = b'c'\).
Dễ thấy hai tam giác AEC và ABD đồng dạng , do đó:
\({{AC} \over {AD}} = {{AE} \over {AB}}\) hay \(bc = l.(l + DE) = {l^2} + l.DE = {l^2} + b'c'\).
Vậy ta có \({l^2} = bc - b'c'\) hay \(l = \sqrt {bc - b'c'} \).
b) Theo tính chất đường phân giác ta có: \({{b'} \over {c'}} = {b \over c}\).
Từ đó, ta có:
\({{b'} \over {b' + c'}} = {b \over {b + c}}\,\,,\,\,{{c'} \over {b' + c'}} = {c \over {b + c}}\). Suy ra \(b' = {{ab} \over {b + c}}\,,\,\,c' = {{ac} \over {b + c}}.\)
Vậy từ câu a), ta có
\(l = \sqrt {bc - {{{a^2}bc} \over {{{(b + c)}^2}}}} = {{\sqrt {bc\left[ {{{(b + c)}^2} - {a^2}} \right]} } \over {b + c}}\).
dapandethi.vn
