Đề bài
Trên các cạnh \(AC\) và \(BC\) của tam giác \(ABC\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \( \dfrac{{AM}}{{MC}} = \dfrac{{NC}}{{NB}} = k\), trên \(MN\) lấy điểm \(P\) sao cho \( \dfrac{{PM}}{{PN}} = k\). Gọi \(S, S_1\) và \(S_2\) lần lượt là diện tích các tam giác \(ABC, APM\) và \(BPN\). Chứng minh \(\sqrt[3]{S} = \sqrt[3]{{{S_1}}} + \sqrt[3]{{{S_2}}}\).
Lời giải chi tiết
(h.137).
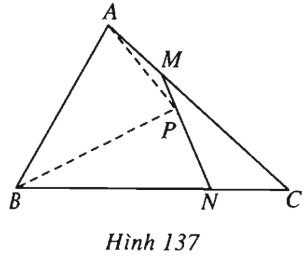
Từ giả thiết\( \dfrac{{AM}}{{MC}} = k\), ta suy ra: \( \dfrac{{AM}}{{AC}} = \dfrac{k}{{k + 1}}\) và \( \dfrac{{MC}}{{AC}} = \dfrac{1}{{k + 1}}\).
Tương tự như thế:
\( \dfrac{{NC}}{{BC}} = \dfrac{k}{{k + 1}} ,\) \( \dfrac{{NB}}{{BC}} = \dfrac{1}{{k + 1}} , \) \( \dfrac{{PM}}{{MN}} = \dfrac{k}{{k + 1}} , \) \( \dfrac{{PN}}{{MN}} = \dfrac{1}{{k + 1}}\).
Từ đó suy ra :
\(\begin{array}{l}{S_1} = {S_{APM}} = \dfrac{k}{{k + 1}}{S_{AMN}} \\= \dfrac{k}{{k + 1}}. \dfrac{k}{{k + 1}}{S_{ACN}}\\ = \dfrac{k}{{k + 1}}. \dfrac{k}{{k + 1}}. \dfrac{k}{{k + 1}}{S_{ABC}}\\ = {\left( { \dfrac{k}{{k + 1}}} \right)^3}S.\end{array}\)
Tính toán tương tự, ta có \({S_2} = {\left( { \dfrac{1}{{k + 1}}} \right)^3}S\).
Vậy \(\sqrt[3]{{{S_1}}} + \sqrt[3]{{{S_2}}} = \dfrac{k}{{k + 1}}\sqrt[3]{S} + \dfrac{1}{{k + 1}}\sqrt[3]{S}\)
\(= \sqrt[3]{S}\).
dapandethi.vn
