Đề bài
Tam giác \(ABC\) có trung tuyến \(AA_1\), đường cao \(BB_1\) và phân giác \(CC_1\) đồng quy. Tìm hệ thức liên hệ giữa ba cạnh của tam giác.
Lời giải chi tiết
(h.136).
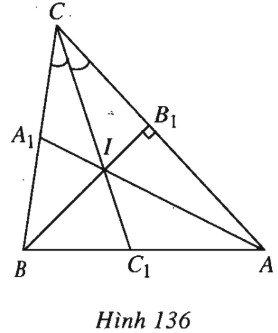
Ta đặt : \(\overrightarrow {CA} = \overrightarrow u , \overrightarrow {CB} = \overrightarrow v \).
Khi đó, \(|\overrightarrow u | = CA , |\overrightarrow v | = CB = a\). Giả sử trung tuyến \(AA_1\) cắt phân giác \(CC_1\) tại \(I\), khi đó \( \dfrac{{IA}}{{I{A_1}}} = \dfrac{{CA}}{{C{A_1}}} = \dfrac{{2b}}{a}\) hay \(a.IA = 2b.I{A_1}\). Vì \(I\) nằm giữa \(A\) và \(A_1\) nên \(a.\overrightarrow {IA} = - 2b.\overrightarrow {I{A_1}} \)
\( \Leftrightarrow a\left( {\overrightarrow {CA} - \overrightarrow {CI} } \right) = - 2\left( {\overrightarrow {C{A_1}} - \overrightarrow {CI} } \right)\)
Suy ra \(\overrightarrow {CI} = \dfrac{{a.\overrightarrow {CA} + 2b\overrightarrow {C{A_1}} }}{{a + 2b}} = \dfrac{{a\overrightarrow u + b\overrightarrow v }}{{a + 2b}}\).
Do đó ta có \(\overrightarrow {BI} = \overrightarrow {CI} - \overrightarrow {CB}\)
\( = \dfrac{{a\overrightarrow u + b\overrightarrow v }}{{a + 2b}} - \overrightarrow v\)
\( = \dfrac{{a\overrightarrow u - (a + b)\overrightarrow v }}{{a + 2b}}\).
Vì đường cao \(BB_1\) đi qua \(I\) nên \(\overrightarrow {BI} .\overrightarrow {CA} = 0\) hay \(\left[ {a\overrightarrow u - (a + b)\overrightarrow v } \right].\overrightarrow u = 0\).
Suy ra
\(\begin{array}{l}a{\overrightarrow u ^2} - (a + b)\overrightarrow u .\overrightarrow v = 0 \\ \Rightarrow a.{b^2} - (a + b)ab\cos C = 0\\ \Rightarrow a{b^2} = \dfrac{1}{2}(a + b)({a^2} + {b^2} - {c^2}) = 0\\ \Rightarrow 2a{b^2} - a\left( {{a^2} + {b^2} - {c^2}} \right) - b\left( {{a^2} + {b^2} - {c^2}} \right) = 0\\ \Rightarrow - a\left( {{a^2} - {b^2} - {c^2}} \right) - b\left( {{a^2} + {b^2} - {c^2}} \right) = 0\end{array}\)
Vậy ta có lien hệ : \(a( - {a^2} + {b^2} + {c^2}) = b({a^2} + {b^2} - {c^2})\).
dapandethi.vn
