Cho ba điểm \(A(-1 ; 0), B(2 ; 4), C(4 ; 1).\)
LG a
Chứng minh rằng tập hợp các điểm \(M\) thỏa mãn \(3M{A^2} + M{B^2} = 2M{C^2}\) là một đường tròn \((C)\). Tìm tọa độ tâm và bán kính của \((C)\).
Lời giải chi tiết:
Xét điểm \(M(x ; y)\). Biến đổi điều kiện \(3M{A^2} + M{B^2} = 2M{C^2}\)qua tọa độ ta được phương trình đường tròn cần tìm \((C): {\left( {x + \dfrac{9}{2}} \right)^2} + {\left( {y - 1} \right)^2} = \dfrac{{107}}{4}\), \((C)\) có tâm \(I\left( { - \dfrac{9}{2} ; 1} \right)\), bán kính \(R = \dfrac{{\sqrt {107} }}{2}\).
LG b
Một đường thẳng \(\Delta \) thay đổi đi qua \(A\) cắt \((C)\) tại \(M\) và \(N\). Hãy viết phương trình của \(\Delta \) sao cho đoạn \(MN\) ngắn nhất.
Lời giải chi tiết:
(h.104).
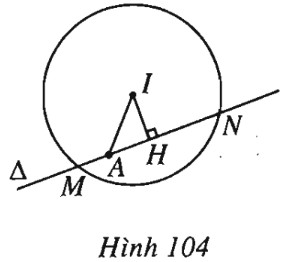
\(IA < R\) nên \(A\) trong \((C)\). Gọi \(H\) là trung điểm của \(MN\) thì \(IH \bot MN\).
\(MN = 2MH = 2\sqrt {{R^2} - I{H^2}} \).
Do đó \(MN\) min \( \Leftrightarrow IH\) max.
Ta luôn có \(IH \le IA\). Vậy \(IH\) max \( \Leftrightarrow H \equiv A\), tức là \(\overrightarrow {IA} = \left( { \dfrac{7}{2} ; - 1} \right)\) là một vectơ pháp tuyến của đường thẳng \(\Delta \) cần tìm. Từ đó suy ra phương trình của \(\Delta \) là \(7x - 2y + 7 = 0\).
dapandethi.vn
