Đề bài
Cho hai đoạn thẳng \(AC\) và \(BD\) cắt nhau tại \(E.\) Biết \(AE.EC = BE.ED\). Chứng minh bốn điểm \(A, B, C, D \)cùng nằm trên một đường tròn.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Các điểm cùng nhìn một cạnh cố định dưới góc bằng nhau thì các điểm đó cùng thuộc một cung chứa góc vẽ trên cạnh cố định.
+) Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.
Lời giải chi tiết
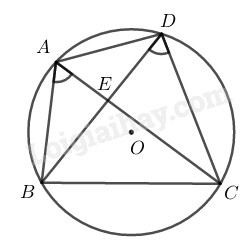
Từ \(AE. EC =BE. ED \;\;(gt)\)
\( \Rightarrow \displaystyle {{AE} \over {ED}} = {{BE} \over {EC}}\)
Xét \(∆AEB\) và \(∆DEC:\)
\(\displaystyle {{AE} \over {ED}} = {{BE} \over {EC}}\)
\(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh)
Suy ra: \(∆AEB\) đồng dạng \(∆DEC\;\; (c.g.c)\)
\( \Rightarrow \widehat {BAE} = \widehat {CDE}\) hay \(\widehat {BAC} = \widehat {CDB}\)
Từ đó: \(A\) và \(D\) nhìn đoạn \(BC\) cố định dưới một góc bằng nhau nên \(4\) điểm \(A,B, C, D\) nằm trên một đường tròn.
dapandethi.vn
