Đề bài
Cho tam giác \(ABC.\) Các đường phân giác trong của \(\widehat B\) và \(\widehat C\) cắt nhau tại \(S,\) các đường phân giác ngoài của \(\widehat B\) và \(\widehat C\) cắt nhau tại \(E.\) Chứng minh \(BSCE\) là một tứ giác nội tiếp.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Hai tia phân giác của hai góc kề bù vuông góc với nhau.
+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng \(180^\circ\) thì tứ giác đó nội tiếp được đường tròn.
Lời giải chi tiết
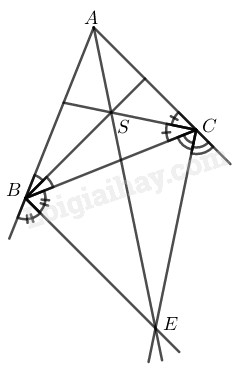
Ta có: \(BS ⊥ BE\) (tính chất: Hai tia phân giác của hai góc kề bù thì vuông góc với nhau)
\( \Rightarrow \widehat {SBE} = 90^\circ \)
Tương tự: \(CS ⊥ CE\) (tính chất: Hai tia phân giác của hai góc kề bù thì vuông góc với nhau)
\( \Rightarrow \widehat {SCE} = 90^\circ \)
Xét tứ giác \(BSCE\) ta có: \(\widehat {SBE} + \widehat {SCE} = 180^\circ \) mà hai góc này ở vị trí đối nhau nên tứ giác \(BSCE\) nội tiếp.
dapandethi.vn
