Đề bài
Cho tam giác cân \(ABC\) có đáy \(BC\) và \(\widehat A = {20^0}\). Trên nửa mặt phẳng bờ \(AB\) không chứa điểm \(C\) lấy điểm \(D\) sao cho \(DA = DB\) và \(\widehat {DAB} = {40^0}\). Gọi \(E\) là giao điểm của \(AB\) và \(CD.\)
\(a)\) Chứng minh \(ACBD\) là tứ giác nội tiếp
\(b)\) Tính \(\widehat {AED}\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng \(180^\circ\) thì tứ giác đó nội tiếp được đường tròn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải chi tiết
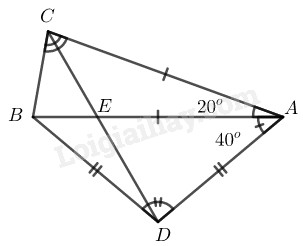
\(a)\) \(∆ABC\) cân tại \(A \;\;(gt).\)
\( \Rightarrow \widehat {ACB} = \widehat {ABC}\) (tính chất tam giác cân)
\( \Rightarrow \widehat {ACB} =\displaystyle {{180^\circ - \widehat A} \over 2} \)\(= \displaystyle {{180^\circ - 20^\circ } \over 2} = 80^\circ \)
\(∆DAB\) cân tại \(D\) (do \(DA=DB)\)
\( \Rightarrow \widehat {DBA} = \widehat {DAB}\) (tính chất tam giác cân) mà \(\widehat {DAB} = 40^\circ \) (gt) \( \Rightarrow \widehat {DBA} = 40^\circ \)
\(\widehat {ADB} = 180^\circ - (\widehat {DAB} + \widehat {DBA})\)\( = 180^\circ - (40^\circ + 40^\circ ) = 100^\circ \)
Trong tứ giác \(ACBD\) ta có: \(\widehat {ACB} + \widehat {ADB} \)\(= 80^\circ + 100^\circ = 180^\circ \)
Vậy: Tứ giác \(ACBD\) nội tiếp.
\(b)\) Vì tứ giác \(ACBD\) nội tiếp (câu a) nên xét đường tròn ngoại tiếp tứ giác \(ACBD\) ta có:
+) \(\widehat {BAC} =\displaystyle {1 \over 2} sđ \overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{BC}\)\( = 2\widehat {BAC} = 2.20^\circ = 40^\circ \)
+) \(\widehat {DBA} =\displaystyle {1 \over 2}sđ \overparen{AD}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AD}\) \( = 2\widehat {DBA} = 2.40^\circ = 80^\circ \)
+) \(\widehat {AED}\) là góc có đỉnh ở trong đường tròn ngoại tiếp tứ giác \(ACBD\)
\(\widehat {AED} =\displaystyle {1 \over 2}(sđ \overparen{BC} + sđ \overparen{AD})\) \( = \displaystyle {{40^\circ + 80^\circ } \over 2} = 60^\circ \)
dapandethi.vn
