Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): \({x^2} + {y^2} - 2x - 2y + 1 = 0\) và đường thẳng \(d:x - y + 3 = 0\). Tìm tọa độ điểm M nằm trên d sao cho đường tròn tâm M có bán kính gấp đôi bán kính đường tròn (C) và tiếp xúc ngoài vơi đường tròn (C).
Phương pháp giải - Xem chi tiết
- Dựng hình, tham số hóa tọa độ điểm \(M\).
- Lập phương trình dựa vào các điều kiện bài cho, giải phương trình và kết luận nghiệm
Lời giải chi tiết
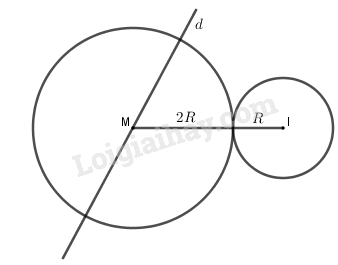
Đường tròn (C) có tâm I(1 ; 1), bán kính R = 1.
Vì \(M \in d\) nên \(M(x;x + 3)\). Yêu cầu của bài toán tương đương với \(MI = R + 2R \) \(\Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {x + 2} \right)^2} = 9\)
\(\begin{array}{l}
\Leftrightarrow {x^2} - 2x + 1 + {x^2} + 4x + 4 = 9\\
\Leftrightarrow 2{x^2} + 2x - 4 = 0
\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\).
Vậy có hai điểm M thỏa mãn yêu cầu bài toán là \(M(1 ; 4)\) và \(M(-2 ; 1)\).
dapandethi.vn
