Bài 3.57 trang 167 SBT hình học 10

Đề bài

Trong mặt phẳng tọa độ Oxy, cho đường tròn  (C) : \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\) và đường thẳng \(d:3x - 4y + m = 0\). Tìm m để trên d có duy nhất một điểm P mà từ đó có thể kẻ được hai tiếp tuyến PA, PB tới (C)  (A, B là các tiếp điểm) sao cho tam giác PAB đều.

Lời giải chi tiết

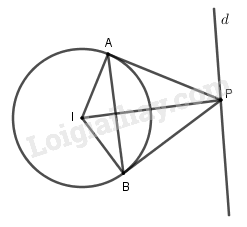
(C) có tâm I(1 ; -2) và bán kính R = 3.

Ta có tam giác PAB đều thì \(IP = 2IA = 2R = 6\) \( \Leftrightarrow P \in \left( {C'} \right)\) tâm I, bán kính \(R' = 6.\) 

Trên d có duy nhất một điểm P thỏa mãn yêu cầu bài toán khi và chỉ khi d tiếp xúc \(\left( {C'} \right)\) tại \(P\) \( \Leftrightarrow d(I,d) = 6\)

\(\begin{array}{l}
\Leftrightarrow \dfrac{{\left| {3.1 - 4.\left( { - 2} \right) + m} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 6\\
\Leftrightarrow \dfrac{{\left| {m + 11} \right|}}{5} = 6\\
\Leftrightarrow \left| {m + 11} \right| = 30\\
\Leftrightarrow \left[ \begin{array}{l}
m + 11 = 30\\
m + 11 = - 30
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
m = 9\\
m = - 41
\end{array} \right.
\end{array}\)

dapandethi.vn