Đề bài
Trong mặt phẳng Oxy cho tam giác ABC cân tại A có \(A(-1;4)\) và các đỉnh B, C thuộc đường thẳng : \(\Delta :x - y - 4 = 0\) .
a) Tính khoảng cách từ A đến đường thẳng \(\Delta \).
b) Xác định tọa độ các điểm B và C, biết diện tích tam giác ABC bằng \(18\).
Phương pháp giải - Xem chi tiết
a) Sử dụng công thức tính khoảng cách từ điểm đến đường thẳng \(d\left( {M,\Delta } \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
b) Sử dụng điều kiện \(AB = AC\) \( \Leftrightarrow B,C\) thuộc đường tròn tâm \(A\) bán kính \(AB = AC\), kết hợp với \(B,C \in \Delta \), lập hệ phương trình và giải hệ suy ra \(B,C\).
Lời giải chi tiết
a) Gọi H là hình chiếu của A trên \(\Delta \), suy ra H là trung điểm của BC.
\(AH = d(A,BC)\) \( = \dfrac{{\left| { - 1 - 4 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{9}{{\sqrt 2 }}\)
b) \(BC = \dfrac{{2{S_{\Delta ABC}}}}{{AH}} \) \( = \dfrac{{2.18}}{{\frac{9}{{\sqrt 2 }}}} = 4\sqrt 2 \)
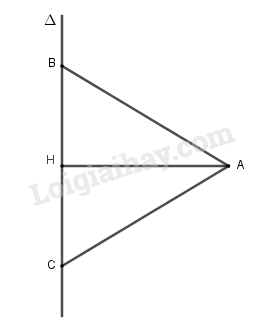
Theo định lí Py-ta-go ta có:
\(AB = AC = \sqrt {A{H^2} + \dfrac{{B{C^2}}}{4}} \) \( = \sqrt {\dfrac{{81}}{2} + \dfrac{{32}}{4}} = \sqrt {\dfrac{{97}}{2}} \)
Do đó \(B,C\) thuộc đường tròn tâm \(A\) bán kính \(AB = \sqrt {\dfrac{{97}}{2}} \).
Phương trình đường tròn \({\left( {x + 1} \right)^2} + {(y - 4)^2} = \dfrac{{97}}{2}\).
Tọa độ điểm B và C là nghiệm của hệ :
\(\left\{ \begin{array}{l}{\left( {x + 1} \right)^2} + {(y - 4)^2} = \dfrac{{97}}{2}\\x - y - 4 = 0\,.\end{array} \right.\)
Giải hệ ta được \(\left( {x;y} \right) = \left( {\dfrac{{11}}{2};\dfrac{3}{2}} \right)\) hoặc \(\left( {x;y} \right) = \left( {\dfrac{3}{2}; - \dfrac{5}{2}} \right)\) .
Vậy \(B\left( {\dfrac{{11}}{2};\dfrac{3}{2}} \right)\,,\,C\left( {\dfrac{3}{2}; - \dfrac{5}{2}} \right)\) hoặc \(B\left( {\dfrac{3}{2}; - \dfrac{5}{2}} \right)\,,C\left( {\dfrac{{11}}{2};\dfrac{3}{2}} \right)\,.\)
dapandethi.vn
