Đề bài
Cạnh góc vuông kề với góc \(60^\circ \) của một tam giác vuông bằng 3. Sử dụng bằng lượng giác của các góc đặc biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư).
Phương pháp giải - Xem chi tiết
Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
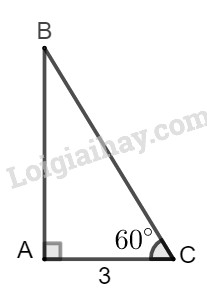
Giả sử tam giác \(ABC\) có \(\widehat A = 90^\circ ,\widehat C = 60^\circ ,AC = 3\).
Ta có: \( \cos {\widehat C}= \dfrac{AC}{BC}\)
\(\Rightarrow BC = \dfrac{AC}{\cos{\widehat C}}= \dfrac{{AC}}{{\cos 60^\circ }} = \dfrac{3}{\displaystyle {{1 \over 2}}} = 6\)
\(\sin 60^\circ = \sin \widehat C = \dfrac{{AB}}{{BC}}\)
Suy ra: \(AB = BC.\sin 60^\circ = 6. \dfrac{{\sqrt 3 }}{2} = 3\sqrt 3. \)
dapandethi.vn
