Đề bài
Vẽ một tam giác vuông có một góc nhọn bằng \(40^0\) rồi viết các tỉ số lượng giác của góc \(40^0\).
Phương pháp giải - Xem chi tiết
Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
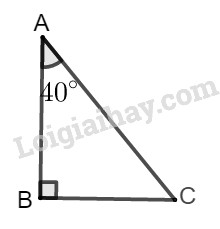
Vẽ tam giác ABC vuông tại B có \(\widehat B= {90^0},\,\widehat A = {40^0}\)
Đặt \(AB = c,AC = b,BC = a.\)
Ta có:
\(\sin 40^\circ = \sin \widehat A = \dfrac{{BC}}{{AC}} = \dfrac{a}{ b}\)
\(\cos 40^0 = \cos \widehat A = \dfrac{{AB}}{{AC}} = \dfrac{c}{ b}\)
\(\displaystyle tg{40^0} = tg\widehat A = {{BC} \over {AB}} = \dfrac{a}{c}\)
\(cotg40^\circ = cotg\widehat A = \dfrac{{AB}}{{BC}} = \dfrac{c }{ a}\)
dapandethi.vn
