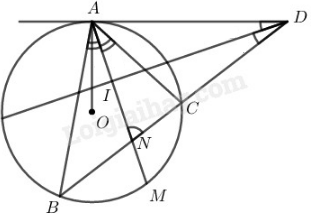
Đề bài
\(A, B, C\) là ba điểm thuộc đường tròn \((O)\) sao cho tiếp tuyến tại \(A\) cắt tia \(BC\) tại \(D.\) Tia phân giác của \(\widehat {BAC}\) cắt đường tròn ở \(M,\) tia phân giác của \(\widehat D\) cắt \(AM\) ở \(I.\) Chứng minh \(DI \bot AM.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Trong tam giác cân, đường phân giác ứng với góc ở đỉnh cũng là đường cao.
Lời giải chi tiết
Ta có: \(\widehat {BAM} = \widehat {MAC}\) (vì \(AM\) là tia phân giác của \(\widehat {BAC}\))
\( \Rightarrow \overparen{BM} =\) \(\overparen{CM}\) \( (1)\)
Ta có: \(\widehat {DAM} = \displaystyle{1 \over 2}sđ \overparen{ACM}\) (góc giữa tia tiếp tuyến và dây cung)
Hay \(\widehat {DAM} = \displaystyle{1 \over 2} (sđ \overparen{AC} + sđ \overparen{CM}\) )\((2)\)
Gọi \(N\) là giao điểm của \(AM\) và \(BC.\)
Ta có: \(\widehat {ANC}\) là góc có đỉnh ở trong đường tròn \((O).\)
\( \Rightarrow \) \(\widehat {ANC} = \displaystyle{1 \over 2} (sđ \overparen{AC} + sđ \overparen{BM})\)\((3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat {DAM} = \widehat {ANC}\) hay \(\widehat {DAN} = \widehat {AND}\)
Suy ra: \(∆DAN\) cân tại \(D\) có \(DI\) là tia phân giác nên suy ra \(DI\) là đường cao
\( \Rightarrow \) \(DI \bot AN\) hay \(DI \bot AM\)
dapandethi.vn