Đề bài
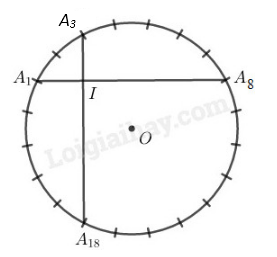
Các điểm \({A_1},{A_2},....,{A_{19}},{A_{20}}\) được sắp xếp theo thứ tự đó trên đường tròn \((O)\) và chia đường tròn thành \(20\) cung bằng nhau. Chứng minh rằng dây \({A_1}{A_8}\) vuông góc với dây \({A_3}{A_{16}}\).
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải chi tiết
Đường tròn \((O)\) được chia thành \(20\) cung bằng nhau nên số đo mỗi cung bằng
\(360^o:20=18^o\)
Gọi giao điểm của \( A_1A_8\) và \( A_3A_{16}\) là \(I.\)
Ta có: \(sđ \overparen{{A_1}{A_3}}\) \( = {2.18^0} = {36^o}\)
\(sđ \overparen{{A_8}{A_{16}}}\) \( = {8.18^0} = {144^o}\)
Ta có: \(\widehat {{A_1}I{A_3}} = \displaystyle {1 \over 2} (sđ \overparen{{A_1}{A_3}} + sđ \overparen{{A_8}{A_{16}}})\) (góc có đỉnh ở trong đường tròn \((O)\))
\( \Rightarrow \) \(\widehat {{A_1}I{A_3}} = \displaystyle {{36^\circ + 144^\circ } \over 2} = 90^\circ \)
\( \Rightarrow A_1A_8 \bot A_3A_{16} \)
dapandethi.vn