Vẽ đồ thị của mỗi hàm số sau và lập bảng biến thiên của nó :
LG a
\(y = \left| {3x + 5} \right|;\)
Lời giải chi tiết:
Ta có:
\(y = \left| {3x + 5} \right| = \left\{ \begin{array}{l}3x + 5\,khi\,x \ge - \frac{5}{3}\\ - 3x - 5\,khi\,x < - \frac{5}{3}\end{array} \right.\)
Đồ thị hàm số \(y = \left| {3x + 5} \right|\) có được bằng cách:
+ Vẽ đường thẳng \(y = 3x + 5\), giữ lại phần đường thẳng ứng với \(x \ge - \frac{5}{3}\).
+ Vẽ đường thẳng \(y = - 3x - 5\), giữ lại phần đường thẳng ứng với \(x < - \frac{5}{3}\).
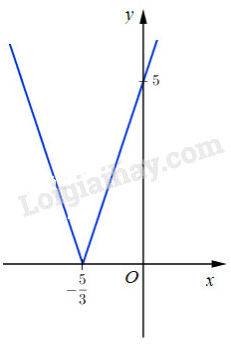
Đồ thị \(y = \left| {3x + 5} \right|\)
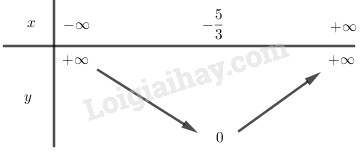
BBT:
LG b
\(y = - 2\left| {x - 1} \right|;\)
Lời giải chi tiết:
Hàm số có thể viết dạng \(y = \left\{ {\matrix{ { - 2x + 2\,\,\,khi\,\,\,x \ge 1} \cr {2x - 2\,\,\,khi\,\,\,x < 1} \cr } .} \right.\)
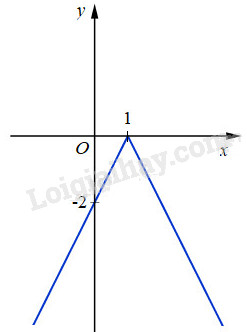
Đồ thị \(y = - 2\left| {x - 1} \right|\)
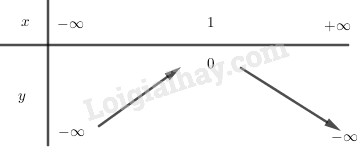
BBT:
LG c
\(y = - {1 \over 2}\left| {2x + 3} \right| + {5 \over 2}.\)
Lời giải chi tiết:
Hàm số có thể viết dạng \(y = \left\{ {\matrix{ { - x + 1\,\,\,khi\,\,\,x \ge - {3 \over 2}} \cr {x + 4\,\,\,khi\,\,\,x < - {3 \over 2}} \cr } .} \right.\)
Đồ thị \(y = - {1 \over 2}\left| {2x + 3} \right| + {5 \over 2}\)
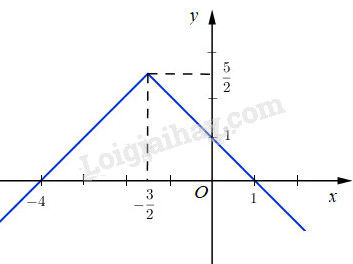
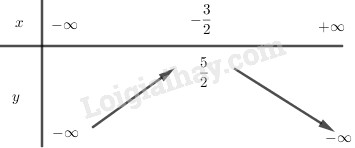
BBT:
dapandethi.vn
