Video hướng dẫn giải
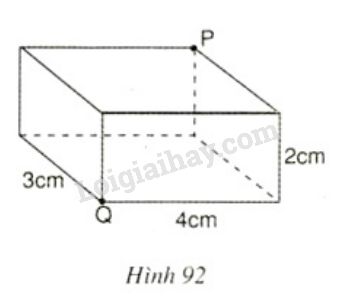
Đố: Các kích thước của một hình hộp chữ nhật là \(4cm,\; 3cm,\; 2cm\). Một con kiến bò theo mặt của hình hộp đó từ \(Q\) đến \(P\) (h.92):
LG a.
Hỏi con kiến bò theo đường nào là ngắn nhất?
Phương pháp giải:
Áp dụng: Định lí Pytago, so sánh hai số vô tỉ.
Giải chi tiết:
Vì con kiến bò theo mặt của hình hộp từ \(Q\) đến \(P\) tức phải bò trên “ một mặt phẳng” ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
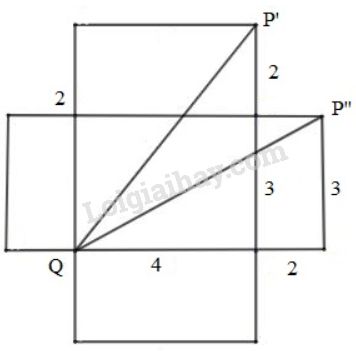
Khi đó, \(P\) sẽ có hai vị trí là \(P’\) và \(P’’\) và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng \(QP’ \) và \(QP’’\) Ta có:
Hình chữ nhật với chiều dài \(2+3=5cm\) và chiều rộng \( 4cm\) có đường chéo \(QP’\) với độ dài:
\(QP’ = \sqrt{4^{2}+ 5^{2}} =\sqrt{41}cm \)
Hình chữ nhật với chiều dài \(4+2=6cm\) và chiều rộng \( 3cm\) có đường chéo \(QP’'\) với độ dài:
\(QP’’ = \sqrt{6^{2}+ 3^{2}}=\sqrt{45}cm \)
Ta có : \( \sqrt{41} < \sqrt{45} \) . Vậy đường đi ngắn nhất là \(QP’\)
LG b.
Độ dài ngắn nhất đó bằng bao nhiêu xentimét?
Phương pháp giải:
Áp dụng: Định lí Pytago, so sánh hai số vô tỉ.
Giải chi tiết:
Vậy độ dài ngắn nhất là \( \sqrt{41} \approx 6,4 cm\) .
dapandethi.vn
