Đề bài
Cho tứ giác \(ABCD.\) Gọi \(E, F, K\) theo thứ tự là trung điểm của \(AD, BC, AC.\)
a) So sánh các độ dài \(EK\) và \(CD, KF\) và \(AB.\)
b) Chứng minh rằng \(EF ≤ \dfrac{AB+CD}{2}\).
Phương pháp giải - Xem chi tiết
Áp dụng:
- Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Trong tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
- Định lí: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
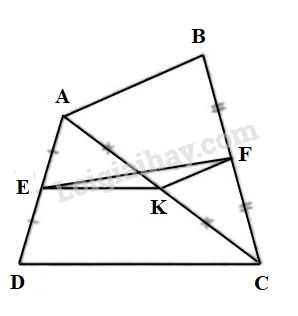

a) \(∆ACD\) có \(EA=ED\) và \( KA=KC\) nên \(EK\) là đường trung bình, suy ra \(EK = \dfrac{CD}{2}\)
\(∆ABC\) có \(KA=KC\) và \(FC=FB\) nên \(KF\) là đường trung bình, suy ra \( KF = \dfrac{AB}{2}\)
b) Ta có: \(EF ≤ EK + KF\)
(theo bất đẳng thức tam giác)
\( \Rightarrow EF ≤ \dfrac{CD}{2} + \dfrac{AB}{2} \)\( \,\Rightarrow EF ≤ \dfrac{AB+CD}{2}\).
Lưu ý. Nếu ba điểm \(E,K,F\) không thẳng hàng thì \(EF<EK+KF\) (bất đẳng thức tam giác)
Nếu \(K\) nằm giữa \(E\) và \(F\) thì \(EF=EK+KF.\)
dapandethi.vn
