Đề bài
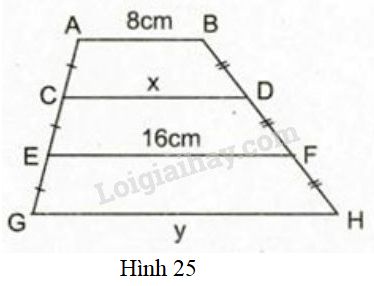
Tính \(x, y\) trên hình \(25\), trong đó \(AB // CD // EF // GH.\)
Phương pháp giải - Xem chi tiết
Áp dụng:
- Hình thang là tứ giác có hai cạnh đối song song.
- Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
Lời giải chi tiết
\(ABFE\) là hình thang vì \(AB // EF\)
Hình thang \(ABFE\) có \(CA = CE\) và \(DB = DF\) nên \( CD\) là đường trung bình của hình thang.
suy ra \( CD = \dfrac{8+16}{2}= 12\,cm.\) Vậy \(x = 12\,cm.\)
Chứng minh tương tự, \( EF\) là đường trung bình của hình thang \(CDHG\) nên \( EF = \dfrac{CD+GH}{2}\)
\(\Rightarrow CD + GH = 2EF \)\(\,\Rightarrow 12 + y = 2.16 \Rightarrow y = 32 - 12 = 20\)
Vậy \( y = 20\,cm.\)
Giải thích thêm: \( EF\) là đường trung bình của hình thang \(CDHG\).
- Vì \(CD // HG\) nên \(CDHG\) là hình thang (dấu hiệu nhận biết hình thang)
Vì \(GE = CE\) (giả thiết) và \(FH = DF\) (giả thiết)
\( \Rightarrow EF\) là đường trung bình của hình thang \(CDHG.\)
dapandethi.vn
