Đề bài
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) và \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều là \(100 N\) và \(\widehat {AMB} = {60^0}\).
a) Đặt \(\overrightarrow {ME} = \overrightarrow {MA} + \overrightarrow {MB} \). Tính độ dài của đoạn \(ME\);
b) Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} \).
Phương pháp giải - Xem chi tiết
a) Dựng hình thoi \(MAEB\) và tính toán.
b) Dựng hình và suy ra kết luận.
Lời giải chi tiết
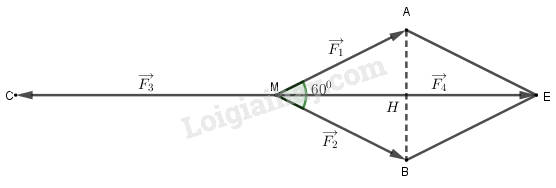
a) Vật đứng yên là do \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \).
Vẽ hình thoi \(MAEB\) ta có: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {ME} \).
Tam giác \(MAB\) là tam giác đều có đường cao \(MH = MA.\cos {30^0} = \dfrac{{100\sqrt 3 }}{2}\)
Suy ra \(ME = 2MH = 100\sqrt 3 \).
b) Lực \(\overrightarrow {{F_4}} = \overrightarrow {ME} \) có cường độ là \(100\sqrt 3 N\).
Ta có \(\overrightarrow {{F_4}} + \overrightarrow {{F_3}} = \overrightarrow 0 \), do đó \(\overrightarrow {{F_3}} \) là vec tơ đối của \(\overrightarrow {{F_4}} \). Như vậy \(\overrightarrow {{F_3}} \) có cường độ là \(100\sqrt 3 N\) và ngược hướng với vec tơ \(\overrightarrow {ME} \).
dapandethi.vn
