Đề bài
Tam giác \(ABC\) có độ dài các cạnh \(AB= m, AC= n\) và \(AD\) là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác \(ABD\) và diện tích tam giác \(ACD\) bằng \(\dfrac{m}{n}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Công thức tính diện tích của tam giác, tính chất đường phân giác của tam giác.
Lời giải chi tiết
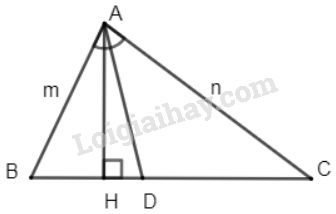
Kẻ \(AH ⊥ BC\)
Ta có:
\({S_{ABD}} = \dfrac{1}{2}AH.BD\)
\({S_{ACD}} = \dfrac{1}{2}AH.DC\)
\( \Rightarrow \dfrac{S_{ABD}}{S_{ACD}} = \dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC} = \dfrac{BD}{DC}\)
Mặt khác: \(AD\) là đường phân giác của \(∆ABC\) (gt)
\( \Rightarrow \dfrac{BD}{DC}= \dfrac{AB}{AC} = \dfrac{m}{n}\) (tính chất đường phân giác của tam giác)
Vậy \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{m}{n}\) (điều phải chứng minh).
dapandethi.vn
