Video hướng dẫn giải
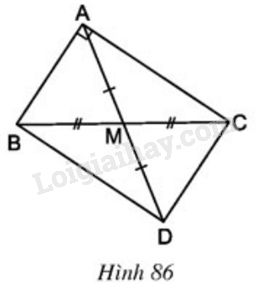
Cho hình \(86\):
LG a.
Tứ giác \(ABDC\) là hình gì? Vì sao?
Phương pháp giải:
Áp dụng:
- Dấu hiệu nhận biết hình bình hành.
- Dấu hiệu nhận biết hình chữ nhật: "Hình bình hành có 1 góc vuông là hình chữ nhật"
Lời giải chi tiết:
Tứ giác \(ABDC\) có hai đường chéo cắt nhau tại trung điểm mỗi đường \(⇒ ABDC\) là hình bình hành.
Hình bình hành \(ABDC\) có góc \(A\) vuông \(⇒ ABDC\) là hình chữ nhật.
LG b.
So sánh các độ dài \(AM\) và \(BC.\)
Phương pháp giải:
Áp dụng tính chất hình chữ nhật.
Lời giải chi tiết:
Vì \(ABDC\) là hình chữ nhật có \(M\) là giao hai đường chéo
\(⇒ AD = BC\) (hai đường chéo bằng nhau) và \(M\) là trung điểm của \(AD, BC\) (tính chất)
\(⇒ \dfrac{{AD}}{2} = \dfrac{{BC}}{2} \Rightarrow AM = \dfrac{{BC}}{2}\)
LG c.
Tam giác vuông \(ABC\) có \(AM\) là đường trung tuyến ứng với cạnh huyền. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lí.
Phương pháp giải:
Từ kết quả câu b để phát biểu định lý.
Lời giải chi tiết:
Định lí: Trong một tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
dapandethi.vn
