Đề bài
Em hãy vẽ hình, viết giả thiết, kết luận và chứng minh định lý trên.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Tính chất tam giác cân.
- Trường hợp bằng nhau của hai tam giác vuông.
- Định nghĩa đường trung trực của đoạn thẳng.
Lời giải chi tiết
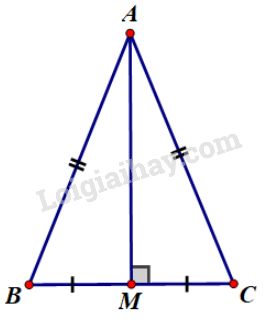

Chứng minh:
Tam giác \(ABC\) cân tại \(A\); Kẻ \(AM \bot BC\) tại \(M\)
Xét hai tam giác vuông \(\Delta AMB\) và \(\Delta AMC\) có:
+) \(AB=AC\) (Vì \(\Delta ABC\) cân tại \(A\))
+) \(\widehat B = \widehat C\) (Vì \(\Delta ABC\) cân tại \(A\))
Suy ra \(\Delta AMB=\Delta AMC\) (cạnh huyền - góc nhọn)
\( \Rightarrow MB = MC\) (hai cạnh tương ứng)
Do đó \(AM\) vừa là đường trung trực đồng thời là đường trung tuyến ứng với cạnh \(BC\) của tam giác \(ABC\).
dapandethi.vn
