Đề bài
Vẽ đường tròn đi qua ba đỉnh của tam giác \(ABC\) trong các trường hợp sau:
a) \(\widehat{A}\), \(\widehat{B}\), \(\widehat{C}\) đều nhọn
b) \(\widehat{A} = {90^0}\)
c) \(\widehat{A} > {90^0}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xác định tâm của đường tròn: Tâm đường tròn chính là giao điểm của hai đường trung trực của hai cạnh bất kì trong tam giác \(ABC\) (cũng là giao điểm của ba trung trực).
Lời giải chi tiết
- Đường tròn đi qua ba đỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Để vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó.
- Tâm của đường tròn là giao điểm của hai đường trung trực (cũng là giao điểm của ba trung trực cần tìm)
* Để vẽ đường tròn ta làm theo các bước sau:
+ Vẽ đường trung trực \(d\) của cạnh \(BC\).
+ Vẽ dường trung trực \(d'\) của cạnh \(AB\).
+ \(d\) cắt \(d'\) tại \(I\) là tâm của đường tròn cần vẽ.
+ Vẽ đường tròn tâm \(I\) bán kính \(IA\) ta được đường tròn cần dựng.
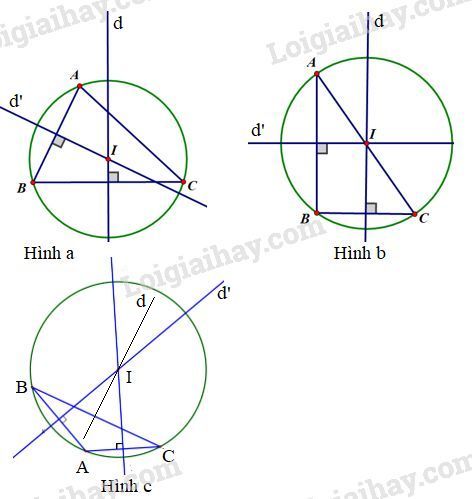
Nhận xét:
- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.
- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền (tâm là trung điểm của cạnh huyền)
- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác.
dapandethi.vn
