Phần câu hỏi bài 6 trang 127 Vở bài tập toán 8 tập 2

Đề bài

Hình lăng trụ đứng tam giác \(ABC.A'B'C'\) có các cạnh bên, cạnh đáy đều bằng nhau và có độ dài bằng \(a\) (h.83).

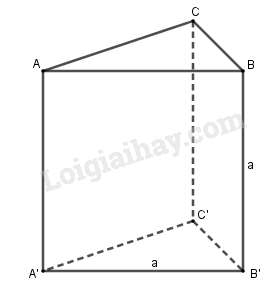
Khoanh tròn vào chữ cái đứng trước câu trả lời đúng.

a) Với \(a = 5cm\), thể tích của hình lăng trụ đứng (lấy đến \(2\) chữ số thập phân) là:

A. \(54,13c{m^3}\)                 B. \(54,12c{m^3}\)

C. \(108,25c{m^3}\)               D. \(108,32c{m^3}\)

b) Với \(a = 6cm\), thể tích của hình lăng trụ đứng (lấy đến \(2\) chữ số thập phân) là:

A. \(93,35c{m^3}\)               B. \(93,53c{m^3}\)

C. \(187,06c{m^3}\)             D. \(187,60c{m^3}\)

c) Với \(a = 7cm\), thể tích của hình lăng trụ đứng (lấy đến \(2\) chữ số thập phân) là:

A. \(297,05c{m^3}\)             B. \(297,50c{m^3}\)

C. \(148,52c{m^3}\)             D. \(148,25c{m^3}\)

Lời giải chi tiết

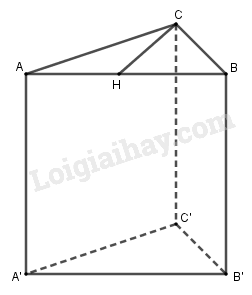
Kẻ \(CH \bot AB\).

\(\Delta ABC\) đều nên \(CH\) là đường cao, đường trung tuyến.

\( \Rightarrow HA = HB = \dfrac{{AB}}{2} = \dfrac{a}{2}\)

Tam giác \(ACH\) vuông tại \(H\) có:

\(A{C^2} = A{H^2} + H{C^2}\) (Py-ta-go)

\( \Rightarrow {a^2} = \dfrac{{{a^2}}}{4} + H{C^2}\) \( \Rightarrow H{C^2} = {a^2} - \dfrac{{{a^2}}}{4} = \dfrac{{3{a^2}}}{4}\) \( \Rightarrow HC = \dfrac{{a\sqrt 3 }}{2}\).

Diện tích tam giác \(ABC\) là:

\({S_{ABC}} = \dfrac{1}{2}CH.AB\) \( = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}.a = \dfrac{{{a^2}\sqrt 3 }}{4}\).

Thể tích hình lăng trụ đứng là:

\(V = Sh = \dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{4}\).

a) Với \(a = 5cm\), thể tích hình lăng trụ đứng là: \(V = \dfrac{{{5^3}.\sqrt 3 }}{4} \approx 54,13\left( {c{m^3}} \right)\)

Chọn A.

b) Với \(a = 6cm\), thể tích hình lăng trụ đứng là: \(V = \dfrac{{{6^3}.\sqrt 3 }}{4} \approx 93,53\left( {c{m^3}} \right)\)

Chọn B.

c) Với \(a = 7cm\), thể tích hình lăng trụ đứng là: \(V = \dfrac{{{7^3}.\sqrt 3 }}{4} \approx 148,52\left( {c{m^3}} \right)\)

Chọn C.

dapandethi.vn