Đề bài
Trong bài toán dựng hình thang cân \(ABCD\;(AB//CD)\) biết \(AB =1,5\,cm, CD=3,5cm,\)\( BD = 3cm\), ta dựng như sau:
- Dựng \(\Delta BDE\) có \(DE=5cm, BD = BE =3cm\).
- Dựng điểm \(C\) trên tia \(DE\) sao cho \(DC = 3,5cm\).
- Dựng đường thẳng \(a\) đi qua \(B\) song song với \(CE\).
- Dựng \(A\) là giao điểm của đường thẳng \(a\) và
(A) đường tròn \((B;1,5cm)\)
(B) đường tròn tâm \(D\) có bán kính bằng \(CB\)
(C) đường tròn \((C;3cm)\)
(D) đường thẳng đi qua \(C\) và song song với \(BE\).
Khoanh tròn vào chữ cái trước câu trả lời đúng.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
Lời giải chi tiết
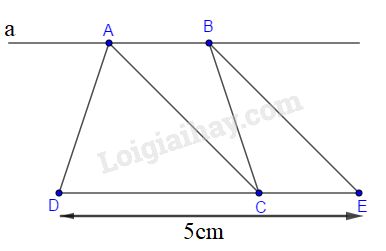
Chọn D.
Đường thẳng đi qua \(C\) và song song với \(BE\) cắt \(a\) tại \(A\) khi đó \(ABEC\) là hình thang có hai cạnh bên song song nên ta có hai cạnh bên \(AC=BE=3cm\).
Do đó hình thang \(ABCD\) có hai đường chéo \(BD=AC=3cm\) nên là hình thang cân (dấu hiệu nhận biết hình thang cân).
Các đáp án (A), (B), (C) đều là đường tròn nên sẽ cắt \(a\) tại hai điểm phân biệt do đó không thỏa mãn bài toán.
dapandethi.vn
