Câu 5.
Khoanh tròn vào chữ cái trước kết quả đúng. Tích của đa thức \({x^2} + 2xy + {y^2}\) với đa thức \({x^2} - 2xy + {y^2}\) là
(A) \({x^4} - {y^4}\)
(B) \({x^4} + 2{x^2}{y^2} - {y^4}\)
(C) \({x^4} - 2{x^2}{y^2} - {y^4}\)
(D) \({x^4} - 2{x^2}{y^2} + {y^4}\)
Phương pháp giải:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Lời giải chi tiết:
\( \left( {{x^2} + 2xy + {y^2}} \right).\left( {{x^2} - 2xy + {y^2}} \right) \)
\( = {x^2}.\left( {{x^2} - 2xy + {y^2}} \right) \)\(+ 2xy.\left( {{x^2} - 2xy + {y^2}} \right) \)\(+ {y^2}.\left( {{x^2} - 2xy + {y^2}} \right) \)
\( = {x^2}.{x^2} + {x^2}.\left( { - 2xy} \right) \)\(+ {x^2}.{y^2} + 2xy.{x^2} + 2xy.\left( { - 2xy} \right)\)\( + 2xy.{y^2} + {y^2}.{x^2} \)\(+ {y^2}.\left( { - 2xy} \right) + {y^2}.{y^2} \)
\( = {x^4} - 2{x^3}y + {x^2}{y^2} + 2{x^3}y - 4{x^2}{y^2} \)\(+ 2x{y^3} + {x^2}{y^2} - 2x{y^3} + {y^4} \)
\( = {x^4} + \left( {2{x^3}y - 2{x^3}y} \right) \)\(+ \left( {{x^2}{y^2} - 4{x^2}{y^2} + {x^2}{y^2}} \right) \)\(+ \left( {2x{y^3} - 2x{y^3}} \right) + {y^4} \)
\(= {x^4} - 2{x^2}{y^2} + {y^4} \)
Chọn D.
Câu 6.
Khoanh tròn vào chữ cái trước kết quả đúng. Giá trị của biểu thức \(M = \left( {{x^2} - {y^2}} \right)\left( {{x^4} + {x^2}{y^2} + {y^4}} \right)\) khi \(x=1;y=0\) là
(A) \(0\) (B) \(-1\)
(C) \(1\) (D) \(2\)
Phương pháp giải:
Bước 1: Thực hiện nhân đa thức với đa thức.
Bước 2: Rút gọn các đơn thức đồng dạng.
Bước 3: Thay \(x=1;y=0\) vào biểu thức rút gọn để tìm giá trị của \(M\).
Lời giải chi tiết:
\( M = \left( {{x^2} - {y^2}} \right)\left( {{x^4} + {x^2}{y^2} + {y^4}} \right) \)
\( = {x^2}.\left( {{x^4} + {x^2}{y^2} + {y^4}} \right)\)\( - {y^2}.\left( {{x^4} + {x^2}{y^2} + {y^4}} \right)\)
\( = {x^2}.{x^4} + {x^2}.{x^2}{y^2} + {x^2}.{y^4} \)\(+ \left( { - {y^2}} \right).{x^4} + \left( { - {y^2}} \right).{x^2}{y^2} \)\(+ \left( { - {y^2}} \right).{y^4}\)
\( = {x^6} + {x^4}{y^2} + {x^2}{y^4} - {x^4}{y^2}\)\( - {x^2}{y^4} - {y^6} \)
\( = {x^6} + \left( {{x^4}{y^2} - {x^4}{y^2}} \right) \)\(+ \left( {{x^2}{y^4} - {x^2}{y^4}} \right) - {y^6} \)
\( = {x^6} - {y^6} \)
- Thay \(x=1;y=0\) vào biểu thức \(M\) ta được:
\(M = {1^6} - {0^6} = 1 - 0 = 1\)
Chọn C.
Câu 7.
Điền dấu "x" vào ô thích hợp
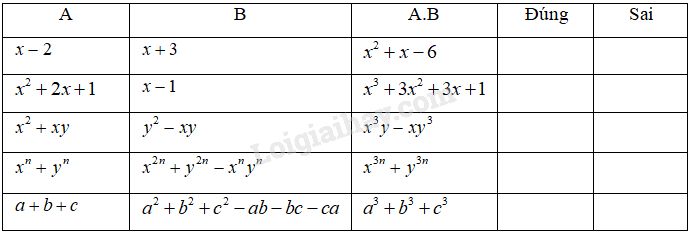
Phương pháp giải:
- Áp dụng quy tắc: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
- Thực hiện thu gọn các đơn thức đồng dạng sau khi thực hiện nhân đa thức với đa thức.
Lời giải chi tiết:
\(\eqalign{
& +)\,\left( {x - 2} \right)\left( {x + 3} \right) \cr
& = x.\left( {x + 3} \right) - 2\left( {x + 3} \right) \cr
& = x.x + x.3 + \left( { - 2} \right).x + \left( { - 2} \right).3 \cr
& = {x^2} + 3x - 2x - 6 \cr
& = {x^2} + \left( {3x - 2x} \right) - 6 \cr
& = {x^2} + x - 6 \cr} \)
\( +)\,\left( {{x^2} + 2x + 1} \right).\left( {x - 1} \right) \)
\(= {x^2}.\left( {x - 1} \right) + 2x.\left( {x - 1} \right) \)\(+ 1.\left( {x - 1} \right) \)
\( = {x^2}.x + {x^2}.\left( { - 1} \right) + 2x.x \)\(+ 2x.\left( { - 1} \right) + 1.x + 1.\left( { - 1} \right) \)
\( = {x^3} - {x^2} + 2{x^2} \)\(- 2x + x - 1 \)
\( = {x^3} + \left( { - {x^2} + 2{x^2}} \right) \)\(+ \left( { - 2x + x} \right) - 1 \)
\(= {x^3} + {x^2} - x - 1 \)
\(+)\, \left( {{x^2} + xy} \right).\left( {{y^2} - xy} \right)\)
\( = {x^2}.\left( {{y^2} - xy} \right) \)\(+ xy.\left( {{y^2} - xy} \right) \)
\(= {x^2}.{y^2} + {x^2}.\left( { - xy} \right) \)\(+ xy.{y^2} + xy.\left( { - xy} \right) \)
\( = {x^2}{y^2} - {x^3}y \)\(+ x{y^3} - {x^2}{y^2} \)
\( = \left( {{x^2}{y^2} - {x^2}{y^2}} \right) \)\(- {x^3}y + x{y^3} \)
\(= - {x^3}y + x{y^3} \)
\( +)\,\left( {{x^n} + {y^n}} \right)\left( {{x^{2n}} + {y^{2n}} - {x^n}{y^n}} \right) \)
\( = {x^n}\left( {{x^{2n}} + {y^{2n}} - {x^n}{y^n}} \right) \)\(+ {y^n}.\left( {{x^{2n}} + {y^{2n}} - {x^n}{y^n}} \right) \)
\( = {x^n}.{x^{2n}} + {x^n}.{y^{2n}} + {x^n}.\left( { - {x^n}{y^n}} \right) \)\(+ {y^n}.{x^{2n}} + {y^n}.{y^{2n}} + {y^n}.\left( { - {x^n}{y^n}} \right) \)
\( = {x^{3n}} + {x^n}{y^{2n}} - {x^{2n}}{y^n} \)\(+ {x^{2n}}{y^n} + {y^{3n}} - {x^n}{y^{2n}} \)
\( = {x^{3n}} + \left( {{x^n}{y^{2n}} - {x^n}{y^{2n}}} \right) \)\(+ \left( {{x^{2n}}{y^n} - {x^{2n}}{y^n}} \right) + {y^{3n}} \)
\( = {x^{3n}} + {y^{3n}} \)
\(+)\, \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) \)
\( = a.\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) \)\( + b.\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right)\)\( + c.\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) \)
\(= a.{a^2} + a.{b^2} + a.{c^2} + a.\left( { - ab} \right) \)\(+ a.\left( { - bc} \right) + a.\left( { - ca} \right) \)\( + b.{a^2} + b.{b^2} + b.{c^2} + b.\left( { - ab} \right) \)\(+ b.\left( { - bc} \right) + b.\left( { - ca} \right) \)\( + c.{a^2} + c.{b^2} + c.{c^2} + c.\left( { - ab} \right) \)\(+ c.\left( { - bc} \right) + c.\left( { - ca} \right) \)
\( = {a^3} + a{b^2} + a{c^2} - {a^2}b \)\(- abc - {a^2}c + {a^2}b + {b^3} \)\( + b{c^2} - a{b^2} - {b^2}c - abc + {a^2}c \)\(+ {b^2}c + {c^3} - abc - b{c^2} - a{c^2} \)
\(= {a^3} + {b^3} + {c^3} + \left( {a{b^2} - a{b^2}} \right) \)\(+ \left( {a{c^2} - a{c^2}} \right) + \left( {{a^2}b - {a^2}b} \right) \)\(+ \left( { - abc - abc - abc} \right) + \left( {{a^2}c - {a^2}c} \right) \)\(+ \left( {b{c^2} - b{c^2}} \right) + \left( {{b^2}c - {b^2}c} \right) \)
\(= {a^3} + {b^3} + {c^3} - 3abc \)
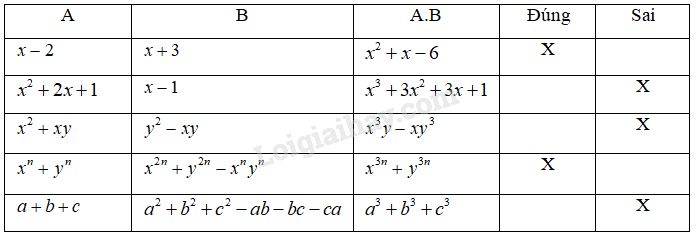
Ta có bảng sau:
dapandethi.vn
