Đề bài
Cho hình binh hành ABCD có M, N, P, Q lần lượt là trung điểm các cạnh AB, BC. CD, DA. Đoạn BQ cắt AP và CM tại R và S, đoạn DN cắt AP và CM tại V và T. Tính ti số diện tích của hai hình bình hành RSTV vả ABCD
Lời giải chi tiết
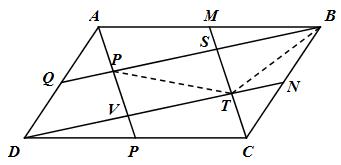
Ta có: QD // BN và \(QP = BN\) (vì \(QD = {{AD} \over 2} = {{BC} \over 2} = BN\))
Do đó tứ giác QBND là hình bình hành \( \Rightarrow QB//DN\)
Chứng minh tương tự ta có AP // MC
Do đó tứ giác RSTV là hình bình hành \( \Rightarrow {S_{RSTV}} = 2{S_{TRS}}\)
\(\Delta ARB\) có MS // AR, AM = BM
\( \Rightarrow RS = BS \Rightarrow {S_{TRS}} = {S_{TBS}}\)
\(\Delta SBC\) có TN // SB, \(BN = CN\)
\( \Rightarrow ST = CT \Rightarrow {S_{TBS}} = {S_{TBC}}\)
Do đó \({S_{RSTV}} = {S_{BCS}}\)
Tương tự \({S_{RSTV}} = {S_{ABR}}\)
\({S_{RSTV}} = {S_{ADV}};\,\,{S_{RSTV}} = {S_{CDT}}\)
Mà \({S_{ABCD}} = {S_{RSTV}} + {S_{BCS}} + {S_{ABR}} + {S_{ADV}} + {S_{CDT}} = 5{S_{RSTV}}\)
Vậy \({{{S_{RSTV}}} \over {{S_{ABCD}}}} = {1 \over 5}\).
dapandethi.vn
