Đề bài
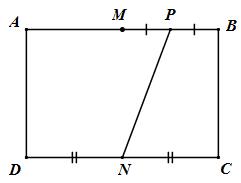
Cho hình chữ nhật ABCD. Gọi M, N, P lần lượt từ trung điềm của AB, CD, MB. Tính tỉ số diện tích hình thang PNCB và hình chữ nhật ABCD.
Lời giải chi tiết
\({{{S_{PNCB}}} \over {{S_{ABCD}}}} = {{{{BC\left( {PB + NC} \right)} \over 2}} \over {BC.AB}} = {{{{PB + NC} \over 2}} \over {AB}} = {{PB + NC} \over {2AB}}\)
\(PB = {1 \over 2}MP\) (P là trung điểm của MB) và \(MB = {1 \over 2}AB\) (M là trung điểm của AB)
Do đó \(PB = {1 \over 2}.{1 \over 2}AB = {1 \over 4}AB\)
\(NC = {1 \over 2}CD\) (N là trung điểm của CD) \( \Rightarrow NC = {1 \over 2}AB\) (ABCD là hình chữ nhật)
Khi đó \({{{S_{PNCB}}} \over {{S_{ABCD}}}} = {{{1 \over 4}AB + {1 \over 2}AB} \over {2AB}} = {{{3 \over 4}AB} \over {2AB}} = {3 \over 8}\)
dapandethi.vn
