Đề bài
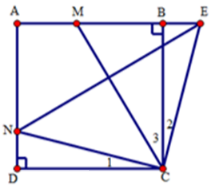
Cho hình vuông ABCD cạnh bằng a có M và N là hai điểm di động lần lượt trên cạnh AB và AD sao cho \(\widehat {MCN} = {45^0}\). Vẽ tia Cx vuông góc với CN,Cx cắt đường thẳng AB tại E.
Chứng minh E là điểm đối xứng của N qua CM.
Phương pháp giải - Xem chi tiết
+ Ta chứng minh \(CE = CN\) suy ra tam giác \(CEN\) cân tại \(C\) .
+ Ta chứng minh CM là tia phân giác đồng thời là trung trực của NE nên E đối xứng với N qua CM.
Lời giải chi tiết
Ta có \(CN \bot CE\,\left( {gt} \right)\) mà \(\widehat {MCN} = {45^0}\) nên \(\widehat {MCE} = {45^0}\) hay \(\widehat {{C_2}} + \widehat {{C_3}} = {45^0}\). Mà \(\widehat {{C_1}} + \widehat {{C_3}} = {45^0}\) (vì \(\widehat {MCN} = {45^0}\)) nên \(\widehat {{C_1}} = \widehat {{C_2}}\).
Xét tam giác CDN và tam giác CBE có:
BC = DC (do ABCD là hình vuông); \(\widehat D = \widehat B = {90^0}\) ; \(\widehat {{C_1}} = \widehat {{C_2}}\) (cmt)
Suy ra \(\Delta CDN = \Delta CBE(g.c.g)\) .Suy ra \(CN = CE\)
Xét tam giác \(CEN\) có \(CN = CE\) (cmt) nên tam giác \(CEN\) là tam giác cân tại \(C.\)
Suy ra phân giác \(CM\) đồng thời là đường trung trực của \(NE .\)
Vậy E là điểm đối xứng của N qua CM.
dapandethi.vn