Xét dấu các biểu thức sau :
LG a
\(\dfrac{1}{{3 - x}} - \dfrac{1}{{3 + {x}}}\)
Lời giải chi tiết:
Biến đổi biểu thức về dạng \(\dfrac{{2{x}}}{{\left( {3 - x} \right)\left( {3 + {x}} \right)}}.\) Học sinh tự lập bảng xét dấu. Kết quả được biểu thức dương khi \(x < -3\) hoặc \(0 < x < 3\) ; biểu thức âm khi \(-3 < x < 0\) hoặc \(x > 3.\)
LG b
\(\dfrac{{{{x}^2} - 6{x} + 8}}{{{x^2} + 8{x} - 9}}\)
Lời giải chi tiết:
\(\dfrac{{{{x}^2} - 6{x} + 8}}{{{x^2} + 8{x} - 9}} = \dfrac{{\left( {{x} - 2} \right)\left( {{x} - 4} \right)}}{{\left( {{x} - 1} \right)\left( {{x} + 9} \right)}}\). Lập bảng xét dấu sau :
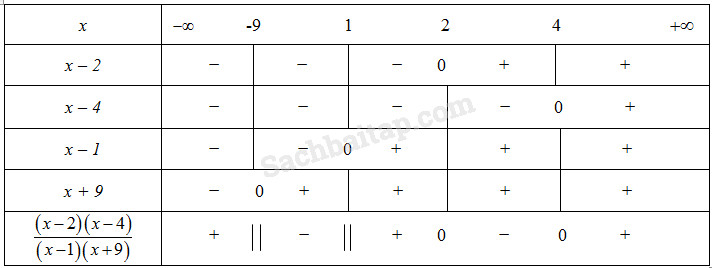
Vậy \(\dfrac{{{{x}^2} - 6{\rm{x}} + 8}}{{{x^2} + 8{x} - 9}} < 0\) khi \(x \in \left( { - 9;1} \right) \cup \left( {2;4} \right)\)
\(\dfrac{{{{x}^2} - 6{x} + 8}}{{{x^2} + 8{x} - 9}} > 0\) khi \(x \in \left( { - \infty ; - 9} \right) \cup \left( {1;2} \right) \cup \left( {4; + \infty } \right)\)
LG c
\(\dfrac{{{{x}^2} + 4{x} + 4}}{{{x^4} - 2{{x}^2}}}\)
Lời giải chi tiết:
Biến đổi biểu thức về dạng \(\dfrac{{{{\left( {{\rm{x}} + 2} \right)}^2}}}{{{x^2}\left( {{{\rm{x}}^2} - 2} \right)}}.\) Từ đó, biểu thức đã cho sẽ dương khi \(x \in \left( { - \infty ; - 2} \right) \cup \left( { - 2; - \sqrt 2 } \right) \cup \left( {\sqrt 2 ; + \infty } \right)\) và sẽ âm khi \(x \in \left( { - \sqrt 2 ;0} \right) \cup \left( {0;\sqrt 2 } \right).\)
LG d
\(\dfrac{{\left| {x + 1} \right| - 1}}{{{x^2} + {x} + 1}}\)
Lời giải chi tiết:
Ta có
\(\dfrac{{\left| {x + 1} \right| - 1}}{{{x^2} + {x} + 1}} = \left\{ {\begin{array}{*{20}{c}}{\dfrac{{x}}{{{x^2} + {x} + 1}}\,khi\,x \ge - 1}\\{\dfrac{{ - x - 2}}{{{x^2} + {x} + 1}}\,khi\,x < - 1}\end{array}} \right.\)
Dấu của biểu thức trên hoàn toàn phụ thuộc vào dấu của tử thức (vì \({x^2} + {x} + 1 > 0\) với mọi x). Vì vậy :
\({{\left| {x + 1} \right| - 1} \over {{x^2} + x + 1}} < 0\) khi \(x \in \left( { - 2;0} \right)\)
và \({{\left| {x + 1} \right| - 1} \over {{x^2} + x + 1}} > 0\) khi \(x \in \left( { - \infty ; - 2} \right) \cup \left( {0; + \infty } \right).\)
dapandethi.vn
