Cho hàm số \(y = \sqrt {{{1 - x} \over x}} \left( {0 < x \le 1} \right)\)
LG a
Tính diện tích hình A giới hạn bởi đồ thị đã cho, trục hoành và đường thẳng \(x = {1 \over 2}\)
Giải chi tiết:
\({\pi \over 4} - {1 \over 2}\)
Hướng dẫn: Đặt \(x = {\sin ^2}t\)
LG b
Tính thể tích khối tròn xoay tạo thành khi quay A xung quanh trục hoành.
Giải chi tiết:
\(\pi \left( {\ln 2 - {1 \over 2}} \right)\)
LG c
Chứng minh rằng \(x = {1 \over {1 + {y^2}}}\) và từ câu a) suy ra giá trị \(\int\limits_0^1 {{{dy} \over {1 + {y^2}}}} \)
Giải chi tiết:
\({\pi \over 4}\)
Hướng dẫn: Giá trị của tích phân là diện tích hình chữ nhật B cộng với diện tích hình A. (h.3.17)
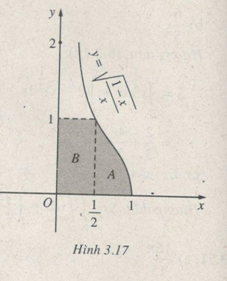
dapandethi.vn
