Đề bài
Tam giác ABC vuông tại A, tia phân giác của \(\widehat B\) cắt AC ở D. So sánh độ dài AD và DC.
Lời giải chi tiết
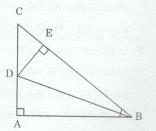
Vẽ \(DE \bot BC\) tại E.
Xét ∆ABD vuông tại A và ∆EBD vuông tại E có: BD (cạnh chung), \(\widehat {ABD} = \widehat {EBD}\) (BD là tia phân giác góc B)
Do đó ∆ABD = ∆EBD (cạnh huyền – góc nhọn) => AD = ED
∆ECD vuông tại E \( \Rightarrow \widehat {CED}\) là góc lớn nhất trong ba góc
=> DC là cạnh lớn nhất trong ba cạnh => DC > ED
Vậy DC > AD.
dapandethi.vn
