Đề bài
Cho tam giác ABC vuông cân tại A có AM là trung tuyến. Lấy điểm D bất kì thuộc cạnh BC. Gọi H và K theo thứ tự là hình chiếu vuông góc cuả B và C xuống đường thẳng AD.
a) Chứng minh tam giác AKC bằng tam giác BHA.
b) Gọi I là giao điểm của Am với CK. Chứng minh đường thẳng DI vuông góc với AC.
c) Chứng minh KM là tia phân giác góc HKI.
Lời giải chi tiết
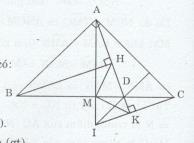
a) Ta có: \(\widehat {BAH} + \widehat {DAC} = 90^\circ (\widehat {BAC} = 90^\circ )\)
\(\widehat {ACK} + \widehat {DAC} = 90^\circ\) (∆AKC vuông tại K)
Do đó \(\widehat {BAH} = \widehat {ACK}\)
Xét ∆AKC (\(\widehat {AKC} = 90^\circ\)) và ∆BHA (\)\widehat {BHA} = 90^\circ\)) có:
AC = AB (∆ABC vuông cân ở A)
Và \(\widehat {ACK} = \widehat {BAH}\)
Do đó: ∆AKC = ∆BHA (cạnh huyền – góc nhọn).
b) ∆ABC cân tại A có AM là đường trung tuyến (gt).
=> AM là đường cao của tam giác ABC. Vậy \(AM \bot BC\) tại M.
∆AIC có: AK là đường cao (\(AK \bot CI\) tại K)
CM là đường cao (\(CM \bot AI\) tại M)
AK cắt CM tại D (gt)
Do đó D là trực tâm của ∆AIC => ID là đường cao của ∆AIC. Vậy \(DI \bot AC.\)
c) ∆AMC vuông tại M (\(AM \bot BC\) tại M) có \(\widehat {ACM} = 45^\circ\) (∆ABC vuông cân tại A)
=> ∆AMC vuông cân tại M => AM = CM
Xét ∆AMH và ∆CMK có AM = CM
\(\widehat {MAH} = \widehat {MCK}\) (cùng phụ với góc AIK)
AH = CK (∆AKC = ∆BHA)
Do đó ∆AMH = ∆CMK (c.g.c) => MH = MK, \(\widehat {AMH} = \widehat {CMK}\)
Ta có \(\widehat {HMK} = \widehat {HMC} + \widehat {CMK} = \widehat {HMC} + \widehat {AMH} = \widehat {AMC} = 90^\circ\)
∆MHK vuông tại M có MH = MK.
=> ∆MHK vuông cân tại M \( \Rightarrow \widehat {MHK} = 45^\circ\). Mà\(\widehat {MKH} + \widehat {MKI} = \widehat {AKI} = 90^\circ\)
Nên \(\widehat {MKI} = 90^\circ - \widehat {MKH} = 90^\circ - 45^\circ = 45^\circ\)
Ta có \(\widehat {MKI} = \widehat {MKH}( = 45^\circ )\).Vậy KM là tia phân giác góc HKI.
dapandethi.vn
