Đề bài
Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(M\) ở ngoài đường tròn đó. Qua điểm \(M\) kẻ hai tiếp tuyến \(MA,\) \(MB\) và cát tuyến \(MCD\) với đường tròn \((O),\) trong đó điểm \(C\) ở giữa hai điểm \(M, D.\) Đường thẳng qua điểm \(C\) và vuông góc với \(OA\) cắt \(AB\) tại \(H.\) Gọi \(I\) là trung điểm của dây \(CD.\) Chứng minh \(HI\) song song với \(AD.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong một đường tròn, đường kính đi trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Các đỉnh của một đa giác cùng nhìn một cạnh dưới một góc vuông thì đa giác đó nội tiếp.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải chi tiết
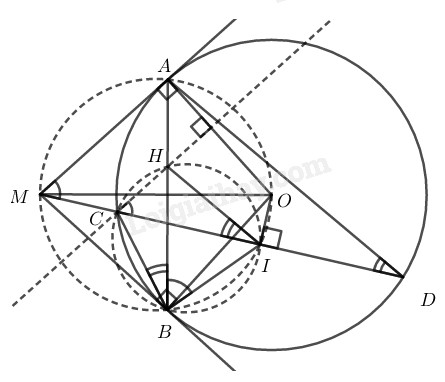
Xét đường tròn \((O)\) có \(MA ⊥ OA\) (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MAO} = 90^\circ \)
\(MB ⊥ OB\) (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MBO} = 90^\circ \)
Lại có I là trung điểm dây CD (gt) nên \(IC = ID\)
\( \Rightarrow OI ⊥ CD\) (đường kính đi qua điểm chính giữa của dây không đi qua tâm thì vuông góc với dây đó)
\( \Rightarrow \widehat {MIO} = 90^\circ \)
Từ đó: \(A, B, I\) nhìn \(MO\) cố định dưới một góc bằng \(90^\circ \) nên \(A, B, I\) nằm trên đường tròn bán kính \(MO.\)
\( \Rightarrow \widehat {AMI} = \widehat {ABI}\) (Hai góc nội tiếp cùng chắn cung nhỏ \(AOI\))
Lại có \( CH ⊥ {AO}\)\(\;\; (gt)\) mà \(MA ⊥ OA\) (chứng minh trên)
Suy ra: \(CH // MA\)
Do đó: \(\widehat {AMI} = \widehat {HCI}\) (hai góc đồng vị)
Suy ra: \(\widehat {HCI} = \widehat {ABI}\) \((=\widehat {AMI})\) hay \(\widehat {HCI} = \widehat {HBI}\)
Do đó \(B\) và \(C\) cùng nằm trên một nửa mặt phẳng bờ chứa đường \(HI\) tạo với \(HI\) một góc bằng nhau nên tứ giác \(BCHI\) nội tiếp.
\( \Rightarrow \widehat {CBH} = \widehat {CIH}\) (hai góc nội tiếp cùng chắn cung nhỏ \(\overparen{CH}\)) hay \(\widehat {CBA} = \widehat {CIH}\)\(\; (1)\)
Trong đường tròn \((O)\) ta có:
\(\widehat {CBA} = \widehat {CDA}\) (\(2\) góc nội tiếp cùng chắn cung nhỏ \(\overparen{AC})\) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {CIH} = \widehat {CDA}\) nên \(HI // AD\) (vì có cặp góc ở vị trí đồng vị bằng nhau)
(Trường hợp cát tuyến đi qua tâm thì ngũ giác \(MAOIB\) suy biến thành tứ giác \(MAOB\) chứng minh tương tự ta có \(HO // AD\)).
dapandethi.vn
