Đề bài
Cho lục giác \(ABCDEF.\) Chứng minh rằng đường chéo \(BF\) chia \(AD\) thành hai đoạn thẳng theo tỉ số \(1: 3.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của nửa đường tròn bằng \(180^o.\)
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Trong hình thoi, hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết
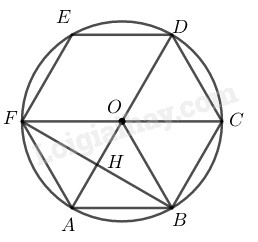
Lục giác đều \(ABCDEF\) nội tiếp trong đường tròn \((O)\)
\(\overparen{AB} = \overparen{CB} = \overparen{CD} = \overparen{DE}\)\( = \overparen{EF}\)\( = \overparen{FA} =60^\circ\)
\( \Rightarrow \) \(sđ \overparen{ABCD}\)\( = sđ \overparen{AB} + sđ \overparen{BC} + sđ \overparen{CD}\)\(=180^\circ\)
Nên \(AD\) là đường kính của đường tròn \((O)\)
Ta có: \(OA = OB = OF = AB = AF = R\)
Nên tứ giác \(ABOF\) là hình thoi
Gọi giao điểm của \(AD\) và \(BF\) là \(H\)
Ta có: \(FB \bot OA\) (tính chất hình thoi)
\( \Rightarrow AH = HO = \displaystyle{{AO} \over 2} = {R \over 2}\)
\(HD = HO + OD = \displaystyle{R \over 2} + R = {\displaystyle{3R} \over 2}\)
Suy ra: \(\displaystyle{{AH} \over {HD}} = {{\displaystyle{R \over 2}} \over {\displaystyle{{3R} \over 2}}} = {1 \over 3}\)
dapandethi.vn
