Đề bài
Cho tam giác nhọn \(ABC\). Vẽ đường tròn (O) có đường kính \(BC\), nó cắt các cạnh \(AB, AC\) theo thứ tự ở \(D, E.\)
a) Chứng minh rằng \(CD \bot AB,BE \bot AC.\)
b) Gọi \(K\) là giao điểm của \(BE\) và \(CD.\) Chứng minh rằng \(AK\) vuông góc với \(BC.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Nếu tam giác \(ABC\) nội tiếp đường tròn tâm \(O,\) trong đó \(BC\) là đường kính thì tam giác \(ABC\) vuông tại \(A.\)
+) Giao của ba đường cao là trực tâm của tam giác.
Lời giải chi tiết
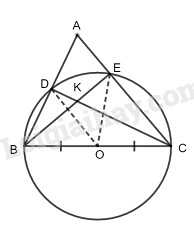
a) Tam giác \(BCD\) nội tiếp trong đường tròn (O) có \(BC\) là đường kính nên vuông tại \(D.\)
Suy ra: \(CD \bot AB\)
Tam giác \(BCE\) nội tiếp trong đường tròn (O) có \(BC\) là đường kính nên vuông tại \(E.\)
Suy ra: \(BE \bot AC\)
b) Xét tam giác \(ABC\) có \(K\) là giao điểm của hai đường cao \(CD\) và \(BE\) nên \(K\) là trực tâm của tam giác \(ABC.\)
Suy ra: \(AK \bot BC\)
dapandethi.vn
