Đề bài
Cho tam giác \(ABC\) nội tiếp đường tròn \((O; R)\) có \(\widehat C = {45^\circ}\).
\(a)\) Tính diện tích hình quạt tròn \(AOB\) (ứng với cung nhỏ \(AB\))
\(b)\) Tính diện tích hình viên phân \(AmB\) (ứng với cung nhỏ \(AB\))
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức: Diện tích hình quạt tròn bán kính \(R,\) cung \(n^\circ\) được tính theo công thức: \(S=\dfrac{\pi R^2n}{360}\).
Lời giải chi tiết
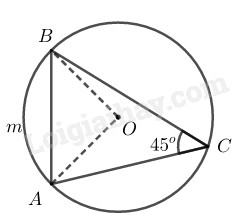
\(a)\) Xét đường tròn \((O)\) có \(\widehat C = {45^\circ }\) \((gt)\) là góc nội tiếp chắn \(\overparen{AmB} \)
\( \Rightarrow sđ \overparen{AmB}= 2.\widehat C\)\(=2.45^0= {90^\circ}\)
Diện tích hình quạt \(AOB\) là:
\(S =\displaystyle {{\pi {R^2}.90} \over {360}} =\displaystyle {{\pi {R^2}} \over 4}\) (đơn vị diện tích)
\(b)\) \(\widehat {AOB} = sđ \overparen{AmB} = {90^0}\)
\( \Rightarrow OA \bot OB\)
Diện tích tam giác \(OAB\) là: \(S =\displaystyle {1 \over 2}OA.OB = \displaystyle {{{R^2}} \over 2}\)
Diện tích hình viên phân \(AmB\) là:
\(S_{qAOB}-S_{AOB}=\displaystyle {{\pi {R^2}} \over 4} - {{{R^2}} \over 2}\)\( =\displaystyle {{{R^2}\left( \displaystyle {\pi - 2} \right)} \over 4}\) (đơn vị diện tích)
dapandethi.vn
