Đề bài
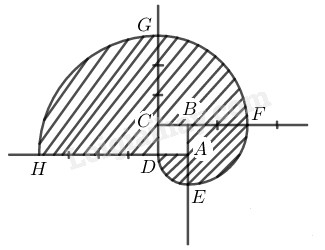
\(a)\) Vẽ đường xoắn \((h.11)\) xuất phát từ một hình vuông cạnh \(1cm.\) Nói cách vẽ.
\(b)\) Tính diện tích hình gạch sọc.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức: Diện tích \(S\) của một hình tròn bán kính \(R\) được tính theo công thức: \(S=\pi.R^2\)
Lời giải chi tiết
\(a)\)
- Vẽ hình vuông \(ABCD\) có cạnh \(1 cm\)
- Vẽ cung đường tròn tâm \(A\) bán kính \(1 cm\) ta được cung \(\overparen{DE}\)
- Vẽ cung đường tròn tâm \(B\) bán kính \(2 cm\) ta được cung \(\overparen{EF}\)
- Vẽ cung đường tròn tâm \(C\) bán kính \(3 cm\) ta được cung \(\overparen{FG}\)
- Vẽ cung đường tròn tâm \(D\) bán kính \(4 cm\) ta được cung \(\overparen{GH}\)
\(b)\) Tính diện tích phần gạch sọc.
Diện tích hình quạt \(DAE = \displaystyle {1 \over 4}\pi {.1^2}\)
Diện tích hình quạt \(EBF = \displaystyle {1 \over 4}\pi {.2^2}\)
Diện tích hình quạt \(FCG = \displaystyle {1 \over 4}\pi {.3^2}\)
Diện tích hình quạt \(GDH =\displaystyle {1 \over 4}\pi {.4^2}\)
Diện tích phần gạch sọc:
\(S = \displaystyle {1 \over 4}\pi \left( {{1^2} + {2^2} + {3^2} + {4^2}} \right) \)\(= \displaystyle{{15} \over 2}(cm^2)\)
dapandethi.vn
